Câu hỏi:
12/07/2024 274
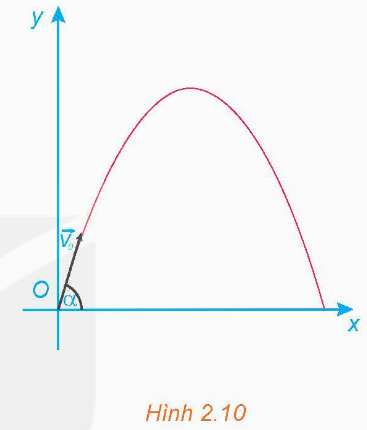
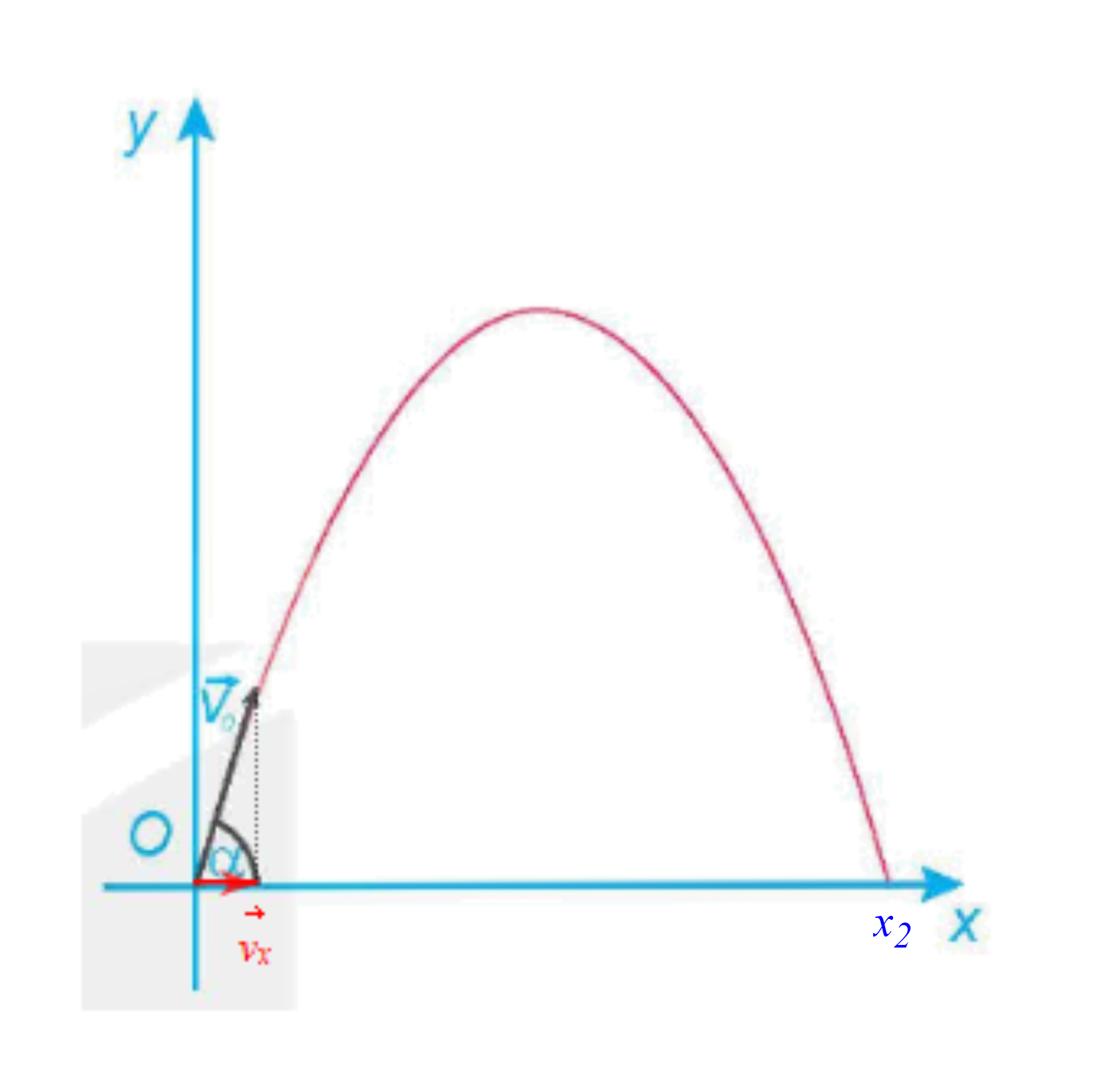
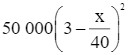Một vật được ném từ mặt đất lên trời xiên góc α so với phương nằm ngang với vận tốc ban đầu v0 = 9 m/s (H.2.10). Khi đó quỹ đạo chuyển động của vật tuân theo phương trình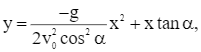 
ở đó x (mét) là khoảng cách vật bay được theo phương ngang từ điểm ném, y (mét) là độ cao so với mặt đất của vật trong quá trình bay, g là gia tốc trọng trường (theo Vật lí đại cương, Nhà xuất bản Giáo dục Việt Nam, 2016).
Tính độ cao nhất của vật trên quỹ đạo và xác định thời điểm mà vật đạt được độ cao đó (giả sử gia tốc trọng trường là g = 9,8 m/s2).
Một vật được ném từ mặt đất lên trời xiên góc α so với phương nằm ngang với vận tốc ban đầu v0 = 9 m/s (H.2.10). Khi đó quỹ đạo chuyển động của vật tuân theo phương trình 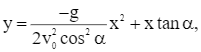ở đó x (mét) là khoảng cách vật bay được theo phương ngang từ điểm ném, y (mét) là độ cao so với mặt đất của vật trong quá trình bay, g là gia tốc trọng trường (theo Vật lí đại cương, Nhà xuất bản Giáo dục Việt Nam, 2016).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta luôn có y ≥ 0 và dễ thấy y = 0 tại x = x1 = 0 và x = x2 (hình vẽ).
Xét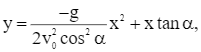 
trên khoảng [0; x2].
Đạo hàm của hàm y là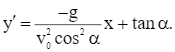 
Ta có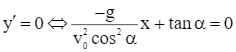 
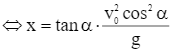
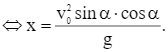
Vận dụng phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn, ta có:
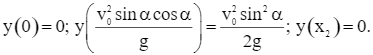
Vì giá trị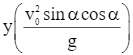 
là giá trị lớn nhất trong ba giá trị trên, nên giá trị lớn nhất của y là 
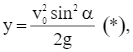đạt được khi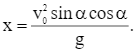 
Từ hình vẽ, ta có vx = v0.cosα, mà x = vx.t nên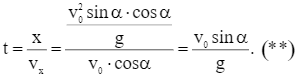 
Thay v0 = 9 m/s và g = 9,8 m/s2 vào (*) và (**) ta được:
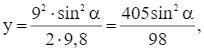tại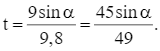 
Vậy vật đạt độ cao nhất trên quỹ đạo là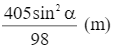 
tại thời điểm 
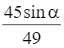(s).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hàm doanh thu là: R(x) = x.p(x) = x.(1 500 – 3x) = 1 500x – 3x2 (nghìn đồng).
Hàm lợi nhuận là:
P(x) = R(x) – C(x) = 1 500x – 3x2 – (18 000 + 500x – 1,6x2 + 0,004x3)
= 1 500x – 3x2 – 18 000 – 500x + 1,6x2 – 0,004x3
= – 0,004x3 – 1,4x2 + 1 000x – 18 000.
Vậy công thức của hàm lợi nhuận là P(x) = – 0,004x3 – 1,4x2 + 1 000x – 18 000 (nghìn đồng).
Lời giải
Hàm doanh thu khi chở x khách hàng là:
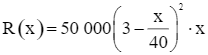
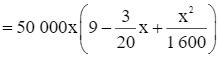
= 450 000x – 7 500x2 + 31,25x3 (đồng) với 0 ≤ x ≤ 60.
Đạo hàm của hàm R(x) là: R’(x) = 450 000 – 15 000x + 93,75x2.
R’(x) = 0 ⇔ 450 000 – 15 000x + 93,75x2 = 0
⇔ x = 120 (không thuộc [0; 60]) hoặc x = 40 (thỏa mãn).
Vận dụng phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn, ta có:
R(0) = 0; R(40) = 8 000 000; R(60) = 6 750 000.
Vì giá trị R(40) là giá trị lớn nhất trong ba giá trị trên, nên giá trị lớn nhất của R(x) đạt được khi x = 40.
Vậy xe có doanh thu cao nhất khi chở 40 hành khách và doanh thu đó bằng 8 000 000 đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận