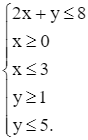Hàm lượng các vi chất (chất vi lượng) calcium, phosphorus và iron chứa trong 100 g hai loại thực phẩm X và Y được cho ở bảng sau:
Calcium (mg)
Phosphorus (mg)
Iron (mg)
X
200
600
8
Y
500
300
6
Từ hai loại thực phẩm X và Y, người ta muốn tạo ra một lượng thực phẩm hỗn hợp chứa ít nhất 2 000 mg calcium, 3 000 mg phosphorus, 48 mg iron. Cần chọn bao nhiêu gam thực phẩm mỗi loại X và Y sao cho lượng thực phẩm hỗn hợp có khối lượng nhỏ nhất?
Hàm lượng các vi chất (chất vi lượng) calcium, phosphorus và iron chứa trong 100 g hai loại thực phẩm X và Y được cho ở bảng sau:
|
|
Calcium (mg) |
Phosphorus (mg) |
Iron (mg) |
|
X |
200 |
600 |
8 |
|
Y |
500 |
300 |
6 |
Từ hai loại thực phẩm X và Y, người ta muốn tạo ra một lượng thực phẩm hỗn hợp chứa ít nhất 2 000 mg calcium, 3 000 mg phosphorus, 48 mg iron. Cần chọn bao nhiêu gam thực phẩm mỗi loại X và Y sao cho lượng thực phẩm hỗn hợp có khối lượng nhỏ nhất?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi x, y (x ≥ 0, y ≥ 0, tính theo gam) lần lượt là số gam thực phẩm loại X và loại Y cần chọn để tạo ra thực phẩm hỗn hợp.
Từ yêu cầu thực phẩm hỗn hợp cần chứa ít nhất 2 000 mg calcium, 3 000 mg phosphorus, 48 mg iron, ta có các bất phương trình
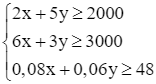hay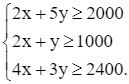 
Lượng thực phẩm hỗn hợp có khối lượng là F = x + y (g).
Từ đó, ta nhận được bài toán quy hoạch tuyến tính:
F = x + y → min
với ràng buộc
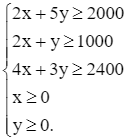
Tập phương án Ω của bài toán là miền không bị gạch chéo trên hình dưới đây, có các đỉnh là A(1 000; 0),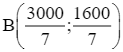 
, C(300; 400) và D(0; 1 000).
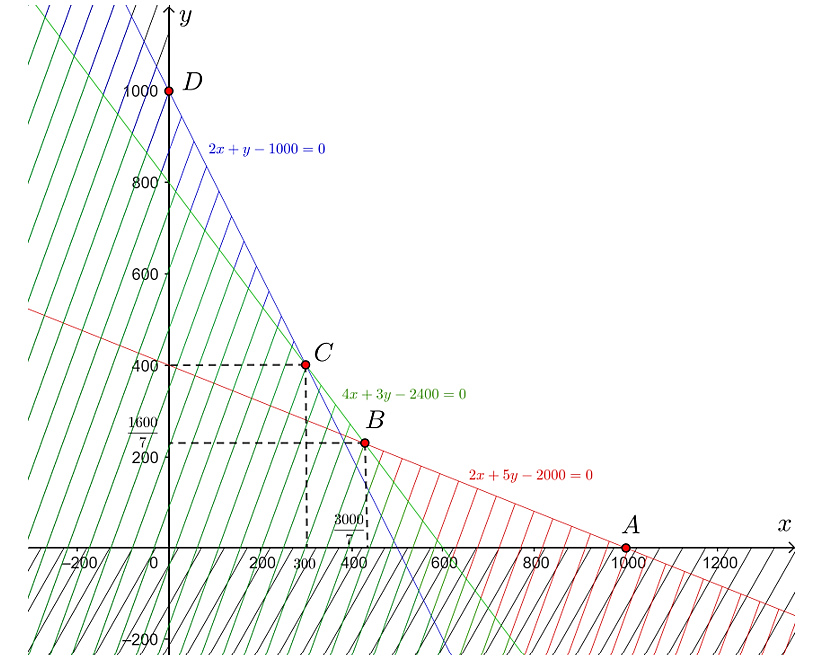
Miền Ω nằm trong góc phần tư thứ nhất, các hệ số của hàm mục tiêu F dương nên F đạt giá trị nhỏ nhất tại đỉnh của Ω.
Giá trị của F tại các đỉnh:
F(1 000; 0) = 1 000 + 0 = 1 000;
;
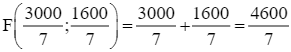F(300; 400) = 300 + 400 = 700;
F(0; 1 000) = 0 + 1 000 = 1 000.
Suy ra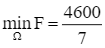 
, đạt được khi 
.
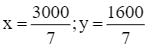Vậy cần dùng 
g thực phẩm loại X và 
g thực phẩm loại Y thì lượng thực phẩm hỗn hợp có khối lượng nhỏ nhất.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi x, y (x ≥ 0, y ≥ 0) lần lượt là số chiếc thuyền loại A và B được đóng trong một tuần.
Khi đó, lợi nhuận thu được mỗi tuần là P = 0,5x + 0,7y (triệu đồng).
Vì mỗi tuần cơ sở bán được tối đa 6 thuyền loại A và tối thiểu 2 thuyền loại B nên ta có x ≤ 6 và y ≥ 2.
Do mỗi tuần cơ sở bổ trí được tối đa 120 giờ lao động cho việc đóng hai loại thuyền nên ta có 10x + 15y ≤ 120 hay 2x + 3y ≤ 24.
Từ đó, ta nhận được bài toán quy hoạch tuyến tính:
P = 0,5x + 0,7y → max
Với ràng buộc
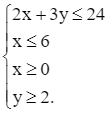
Tập phương án Ω của bài toán là miền tứ giác ABCD được tô màu như hình dưới đây với các đỉnh A(0; 2), B(6; 2), C(6; 4) và D(0; 8).
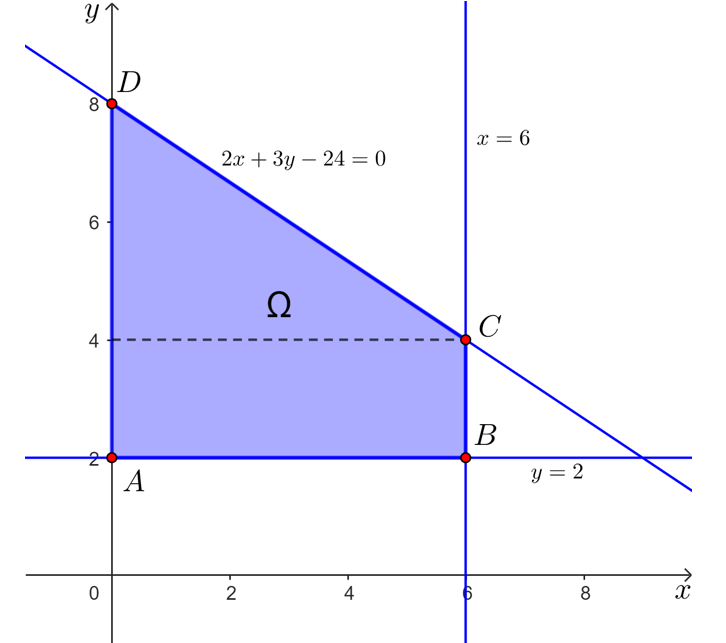
Giá trị của P tại các đỉnh:
P(0; 2) = 0,5 ∙ 0 + 0,7 ∙ 2 = 1,4;
P(6; 2) = 0,5 ∙ 6 + 0,7 ∙ 2 = 4,4;
P(6; 4) = 0,5 ∙ 6 + 0,7 ∙ 4 = 5,8;
P(0; 8) = 0,5 ∙ 0 + 0,7 ∙ 8 = 5,6.
Do đó, 
, đạt được khi x = 6, y = 4.
Vậy mỗi tuần cơ sở đó nên đóng 6 chiếc thuyền loại A và 4 chiếc thuyền loại B thì thu được lợi nhuận cao nhất là 5,8 triệu đồng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi x, y (x ≥ 0, y ≥ 0, tính theo tấn) lần lượt là khối lượng sản phẩm loại A và sản phẩm loại B cần sản xuất. Khi đó lợi nhuận thu được là P = 0,05x + 0,09y (triệu đồng).
Vì xí nghiệp sản xuất sản lượng sản phẩm loại A không ít hơn 3 lần sản lượng sản phẩm loại B nên x ≥ 3y.
Do thời gian để làm việc của dây chuyền không quá 6 giờ nên 0,02x + 0,03y ≤ 6.
Từ đó, ta nhận được bài toán quy hoạch tuyến tính:
P = 0,05x + 0,09y → max
với ràng buộc
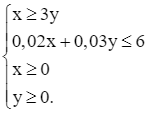
Tập phương án Ω của bài toán là miền tam giác OAB trên hình dưới đây với các đỉnh O(0; 0), A(300; 0) và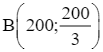 
.
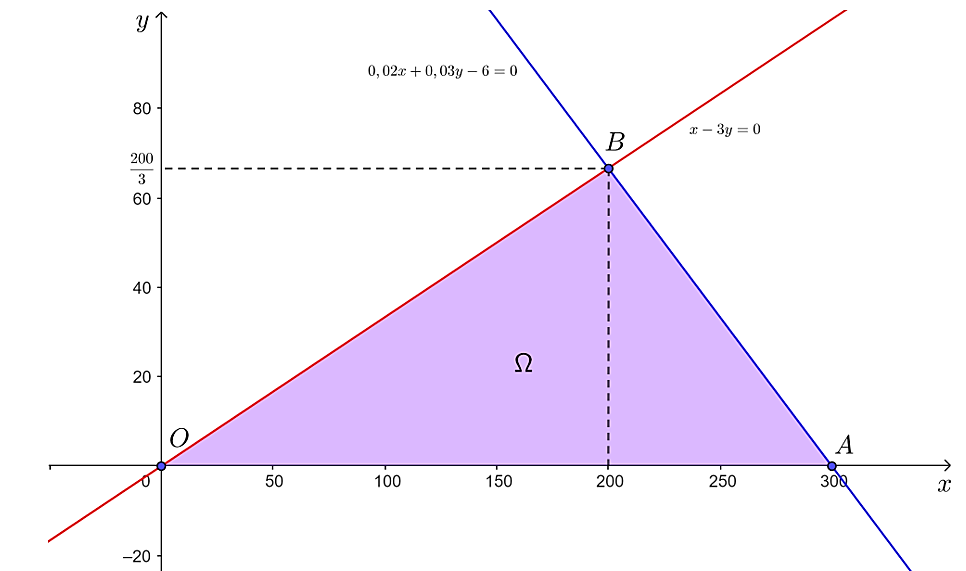
Giá trị của P tại các đỉnh:
P(0; 0) = 0;
P(300; 0) = 0,05 ∙ 300 + 0,09 ∙ 0 = 15;
.
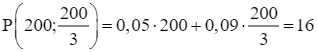Do đó, 
, đạt được khi x = 200,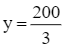 
.
Vậy trong thời gian không quá 6 giờ làm việc của dây chuyền, cần sản xuất 200 tấn sản phẩm loại A và 
tấn sản phẩm loại B để thu được lợi nhuận cao nhất.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập