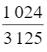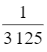Câu hỏi:

13/07/2024 167

Vào đầu mùa đông, trang trại A lắp mới 10 bóng đèn để sưởi ấm cho gà. Các bóng đèn hoạt động độc lập với nhau và sẽ được bật liên tục trong mùa đông. Bóng bị hỏng không được thay thế. Xác suất không bị hỏng trong cả mùa đông của mỗi bóng đều bằng 0,8. Đàn gà sẽ đủ ấm nếu có ít nhất 7 bóng đèn hoạt động.

Tính xác suất của biến cố “Đàn gà đủ ấm trong suốt mùa đông”.

Xem lời giải

Câu hỏi trong đề: Giải chuyên đề Toán 12 CTST Bài 2. Phân bố Bernoulli và phân bố nhị thức có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Gọi T là phép thử “Lắp ngẫu nhiên một bóng đèn” và A là biến cố “Bóng đèn A hoạt động”. Gọi X là số lần xảy ra biến cố A khi lặp lại 10 lần phép thử T.

Do phép thử T được thực hiện 10 lần một cách độc lập với nhau và xác suất của biến cố A trong mỗi lần thử đều bằng 0,8 nên X là biến cố ngẫu nhiên rời rạc có phân bố nhị thức B(10; 0,8). Do đó:

với k = 0, 1, …, 10.

Do đàn gà sẽ đủ ấm suốt mùa đông nếu có ít nhất 7 bóng đèn hoạt động nên ta có:

P(X ≥ 7) = P(X = 7) + P(X = 8) + P(X = 9) + P(X = 10)

≈ 0,201 + 0,302 + 0,268 + 0,107 = 0,878.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho biến ngẫu nhiên rời rạc X có phân bố nhị thức B(5; 0,2).

Tính kì vọng và độ lệch chuẩn của X.

Xem đáp án

Lời giải

Ta có với k = 0, 1, 2, 3, 4, 5.

Lần lượt tính P(X = k) với k = 0, 1, 2, 3, 4, 5 từ công thức trên, ta thu được bảng phân bố xác suất của X như sau:

X	0	1	2	3	4	5
P

Kì vọng của X là:

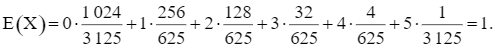
Phương sai của X là:

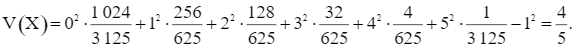
Độ lệch chuẩn của X là:

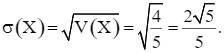
Chú ý: Ta cũng có thể tính kì vọng và phương sai của X như sau:

E(X) = np = 5 . 0,2 = 1 và V(X) = np(1 – p) = 5 . 0,2 . (1 – 0,2) = 0,8.

Do đó độ lệch chuẩn của X là: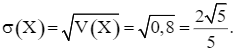

Câu 2

Tỉ lệ người lao động có bằng đại học ở một khu công nghiệp là 30%. Tiến hành phỏng vấn lần lượt 10 người lao động được lựa chọn ngẫu nhiên một cách độc lập từ khu công nghiệp đó. Tính xác suất của các biến cố sau:

A: “Có đúng 3 trong 10 người được phỏng vấn có bằng đại học”;

B: “Có ít nhất 1 trong 10 người được phỏng vấn có bằng đại học”.

Xem đáp án

Lời giải

Gọi T là phép thử “Phỏng vấn ngẫu nhiên một người lao động từ khi công nghiệp”. Theo đề bài, phép thử T được lặp lại 10 lần một cách độc lập. Gọi X là biến cố “Người lao động có bằng đại học”. Ta có P(X) = 30% = 0,3.

Gọi Xk là biến cố “Có k người có bằng đại học trong 10 người lao động được phỏng vấn”, với k = 0, 1, …, 10. Áp dụng công thức Bernoulli, ta có:

với k = 0, 1, …, 10.

Do đó,

Ta có

Câu 3