Một hộp có 24 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 24; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét biết cố A: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” và biến cố B: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”.
Viết các tập con của không gian mẫu tương ứng với các biến cố A, B, A ∩ B, 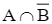 (Hình 1).
(Hình 1).
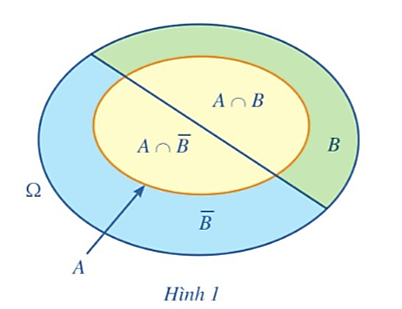
Viết các tập con của không gian mẫu tương ứng với các biến cố A, B, A ∩ B, ![]() (Hình 1).
(Hình 1).

Quảng cáo
Trả lời:
Ω = {1; 2; 3; …; 24}.
A = {3; 6; 9; 12; 15; 18; 21; 24}.
B = {4; 8; 12; 16; 20; 24}.
A ∩ B = {12; 24}.
![]() = {1; 2; 3; 5; 6; 7; 9; 10; 11; 13; 14; 15; 17; 18; 19; 21; 22; 23}.
= {1; 2; 3; 5; 6; 7; 9; 10; 11; 13; 14; 15; 17; 18; 19; 21; 22; 23}.
A ∩ ![]() = {3; 6; 9; 15; 18; 21}.
= {3; 6; 9; 15; 18; 21}.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét hai biến cố:
A: “Con bò được chọn ra không bị mắc bệnh bò điên”.
B: “Con bò được chọn ra có phản ứng dương tính”.
Vì tỉ lệ bò bị mắc bệnh bò điên ở Hà Lan là 13 con trên 1 000 000 con nên tỉ lệ bò mắc bệnh bò điên ở Hà Lan là P(![]() ) = 0,000013.
) = 0,000013.
Suy ra P(A) = 1 – 0,000013 = 0,999987.
Trong số những con bò không bị mắc bệnh thì xác suất để có phản ứng dương tính trong xét nghiệm A là 10%, suy ra P(B | A) = 0,1.
Khi con bò mắc bệnh bò điên thì xác suất để có phản ứng dương tính trong xét nghiệm A là 70% nên P(B | ![]() ) = 0,7.
) = 0,7.
Ta thấy xác suất mắc bệnh bò điên của một con bò ở Hà Lan xét nghiệm có phản ứng dương tính với xét nghiệm A chính là P(![]() | B). Áp dụng công thức Bayes, ta có:
| B). Áp dụng công thức Bayes, ta có:
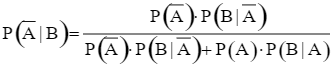
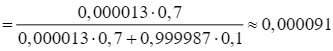 .
.
Vậy khi một con bò ở Hà Lan có phản ứng dương tính với xét nghiệm A thì xác suất để nó bị mắc bệnh bò điên là 0,000091.
Lời giải
Xét hai biến cố:
A: “Người được chọn là đàn ông”;
B: “Người được chọn bị mù màu”.
Theo bài ra ta có: P(B | A) = 0,05; P(B | ![]() ) = 0,0025.
) = 0,0025.
Vì số đàn ông bằng số phụ nữ nên ta có P(A) = 0,5 và P(![]() ) = 1 – 0,5 = 0,5.
) = 1 – 0,5 = 0,5.
Áp dụng công thức Bayes, ta có xác suất để một người mù màu được chọn là đàn ông là: P(A | B) = 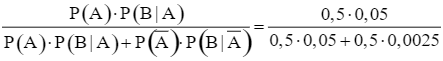 ≈ 0,9524.
≈ 0,9524.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.