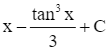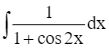Câu hỏi:
13/07/2024 597
Một vườn ươm cây cảnh bán một cây sau 6 năm trồng và uốn tạo dáng. Tốc độ tăng trưởng trong suốt 6 năm được tính xấp xỉ bởi công thức h'(t) = 1,5t + 5, trong đó h(t) (cm) là chiều cao của cây sau t (năm) (Nguồn: R. Larson and B. Edwards, Calculus 10e Cengage 2014). Biết rằng, cây con khi được trồng cao 12 cm.
Khi được bán, cây cao bao nhiêu centimét?
Một vườn ươm cây cảnh bán một cây sau 6 năm trồng và uốn tạo dáng. Tốc độ tăng trưởng trong suốt 6 năm được tính xấp xỉ bởi công thức h'(t) = 1,5t + 5, trong đó h(t) (cm) là chiều cao của cây sau t (năm) (Nguồn: R. Larson and B. Edwards, Calculus 10e Cengage 2014). Biết rằng, cây con khi được trồng cao 12 cm.
Khi được bán, cây cao bao nhiêu centimét?Câu hỏi trong đề: Giải SGK Toán 12 CD Bài 1. Nguyên hàm có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Khi cây được bán, tức là t = 6, ta có h(6) = 0,75 ∙ 62 + 5 ∙ 6 + 12 = 69.
Vậy khi được bán, cây cao 69 cm.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hàm số P(t) là một nguyên hàm của hàm số P'(t).
Ta có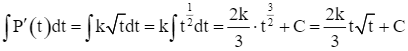 
.
Suy ra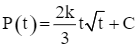 
.
Quần thể vi khuẩn ban đầu gồm 500 vi khuẩn nên với t = 0 thì P = 500 hay P(0) = 500, suy ra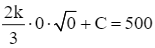 
, do đó C = 500.
Suy ra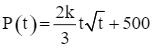 
.
Vì sau 1 ngày, số lượng vi khuẩn của quần thể đó đã tăng lên thành 600 vi khuẩn, tức là khi t = 1 thì P = 600, hay P(1) = 600, suy ra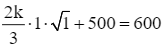 
, do đó k = 150.
Khi đó, công thức tính số lượng vi khuẩn của quần thể đó tại thời điểm t là:
.
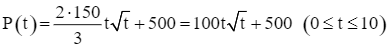Vậy số lượng vi khuẩn của quần thể đó sau 7 ngày là:
(vi khuẩn).
Lời giải
Hàm số M(t) là một nguyên hàm của hàm số m(t).
Ta có 
.
Suy ra M(t) = 800t – t2 + C.
Tại t = 0 thì M(t) = M(0) = 0.
Do đó 800 ∙ 0 – 02 + C = 0, suy ra C = 0.
Khi đó, M(t) = 800t – t2 (0 ≤ t ≤ 400).
Số ngày công tính đến khi hoàn thành dự án là
M(400) = 800 ∙ 400 – 4002 = 160 000 (ngày công).
Chi phí nhân công lao động của công trình đó (cho đến lúc hoàn thành dự án) là
160 000 ∙ 400 000 = 6,4 ∙ 1010 (đồng) = 64 (tỷ đồng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận