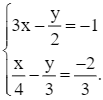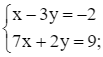Hai khu công nghiệp A và B có tổng cộng 2 200 công nhân. Sau khi chuyển 100 công nhân ở khu A sang khu B thì 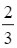 số công nhân ở khu A bằng
số công nhân ở khu A bằng 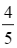 số công nhân ở khu B. Tính số công nhân ở mỗi khu công nghiệp lúc ban đầu.
số công nhân ở khu B. Tính số công nhân ở mỗi khu công nghiệp lúc ban đầu.
Hai khu công nghiệp A và B có tổng cộng 2 200 công nhân. Sau khi chuyển 100 công nhân ở khu A sang khu B thì ![]() số công nhân ở khu A bằng
số công nhân ở khu A bằng ![]() số công nhân ở khu B. Tính số công nhân ở mỗi khu công nghiệp lúc ban đầu.
số công nhân ở khu B. Tính số công nhân ở mỗi khu công nghiệp lúc ban đầu.
Câu hỏi trong đề: Giải SBT Toán 9 CD Bài tập cuối chương 1 có đáp án !!
Quảng cáo
Trả lời:
Gọi x, y (công nhân) lần lượt là số công nhân ở khu công nghiệp A, khu công nghiệp B lúc ban đầu với x, y ∈ ℕ*.
Theo bài, hai khu công nghiệp A và B có tổng cộng 2 200 công nhân nên ta có phương trình: x + y = 2 200. (1)
Khi chuyển 100 công nhân ở khu A sang khu B thì:
⦁ số công nhân ở khu A lúc này là x – 100 (công nhân), do đó ![]() số công nhân ở khu A là
số công nhân ở khu A là 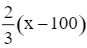 (công nhân).
(công nhân).
⦁ số công nhân ở khu B lúc này là y + 100 (công nhân), do đó ![]() số công nhân ở khu B là
số công nhân ở khu B là 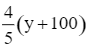 (công nhân).
(công nhân).
Theo bài, sau khi chuyển 100 công nhân ở khu A sang khu B thì ![]() số công nhân ở khu A bằng
số công nhân ở khu A bằng ![]() số công nhân ở khu B nên ta có phương trình:
số công nhân ở khu B nên ta có phương trình:
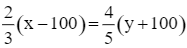
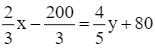
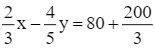
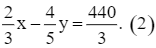
Từ (1) và (2), ta có hệ phương trình: 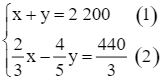
Nhân hai vế của phương trình (1) với 2 và nhân hai vế của phương trình (2) với 3, ta được hệ phương trình sau:
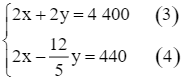
Trừ từng vế hai phương trình (3) và (4), ta nhận được phương trình:
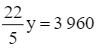 hay y = 900.
hay y = 900.
Thay y = 900 vào phương trình (1) ta có: x + 900 = 2 200 hay x = 1 300.
Ta thấy x = 1 300, y = 900 thỏa mãn điều kiện.
Vậy số công nhân ở khu công nghiệp A và khu công nghiệp B lúc ban đầu lần lượt là 1 300 công nhân và 900 công nhân.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đổi 4 giờ 48 phút = 4,8 giờ.
Gọi x (giờ), y (giờ) lần lượt là thời gian vòi thứ nhất và vòi thứ hai chảy một mình được đầy bể (điều kiện x > 4,8 và y > 4,8).
⦁ Trong 1 giờ, vòi thứ nhất chảy một mình được ![]() (bể), vòi thứ hai chảy một mình được
(bể), vòi thứ hai chảy một mình được ![]() (bể).
(bể).
Hai vòi nước cùng chảy vào một bể sau 4 giờ 48 phút giờ sẽ đầy, nên trong 1 giờ hai vòi cùng chảy thì được 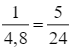 bể, ta có phương trình:
bể, ta có phương trình:
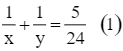
⦁ Trong 4 giờ vòi thứ nhất chảy một mình được ![]() (bể).
(bể).
Trong 3 giờ vòi thứ hai chảy một mình được ![]() (bể).
(bể).
Theo bài, nếu vòi thứ nhất chảy trong 4 giờ, vòi thứ hai chảy trong 3 giờ thì cả hai vòi chảy được ![]() bể nên ta có phương trình:
bể nên ta có phương trình:
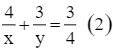
Từ (1) và (2) ta có hệ phương trình: 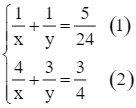
Nhân hai vế của phương trình (1) với 4, ta được hệ phương trình sau:
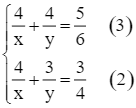
Trừ từng vế của phương trình (3) và (2), ta nhận được phương trình sau:
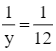 nên y = 12.
nên y = 12.
Thay y = 12 vào phương trình (1), ta được: 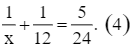
Giải phương trình (4):
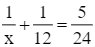
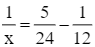
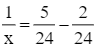
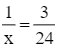
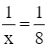
x = 8.
Ta thấy x = 8 và y = 12 thỏa mãn điều kiện.
Vậy thời gian chảy riêng một mình để đầy bể của vòi thứ nhất và vòi thứ hai lần lượt là 8 giờ và 12 giờ.
Lời giải
Gọi x (km/h), y (km/h) lần lượt là tốc độ của xe máy thứ nhất, xe máy thứ hai với x > 0, y > 0.
Theo bài, tốc độ của xe máy thứ hai bằng ![]() tốc độ của xe máy thứ nhất nên ta có phương trình:
tốc độ của xe máy thứ nhất nên ta có phương trình: 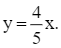
Sau 2 giờ, xe máy thứ nhất đi được quãng đường là: 2x (km) và xe máy thứ hai đi được quãng đường là: 2y (km).
Vì sau 2 giờ hai xe gặp nhau nên ta có:
2x + 2y = AB (trong đó AB là độ dài quãng đường AB).
Ta lập được hệ phương trình: 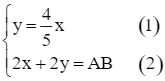
Thế (1) vào phương trình (2), ta nhận được phương trình:
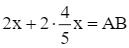
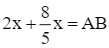
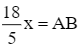
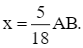
Thay 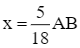 vào phương trình (1), ta được:
vào phương trình (1), ta được:
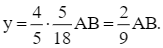
Như vậy, xe máy thứ nhất đi cả quãng đường AB trong: 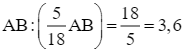 (giờ); xe máy thứ hai đi cả quãng đường AB trong:
(giờ); xe máy thứ hai đi cả quãng đường AB trong: 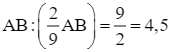 (giờ).
(giờ).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.