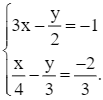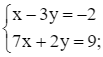Hai xe máy khởi hành cùng một lúc. Xe máy thứ nhất đi từ địa điểm A đến địa điểm B và xe máy thứ hai đi từ địa điểm B đến địa điểm A (trên cùng quãng đường). Tốc độ của xe máy thứ hai bằng 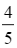 tốc độ của xe máy thứ nhất và sau 2 giờ hai xe gặp nhau. Hỏi mỗi xe đi cả quãng đường AB trong bao lâu?
tốc độ của xe máy thứ nhất và sau 2 giờ hai xe gặp nhau. Hỏi mỗi xe đi cả quãng đường AB trong bao lâu?
Hai xe máy khởi hành cùng một lúc. Xe máy thứ nhất đi từ địa điểm A đến địa điểm B và xe máy thứ hai đi từ địa điểm B đến địa điểm A (trên cùng quãng đường). Tốc độ của xe máy thứ hai bằng ![]() tốc độ của xe máy thứ nhất và sau 2 giờ hai xe gặp nhau. Hỏi mỗi xe đi cả quãng đường AB trong bao lâu?
tốc độ của xe máy thứ nhất và sau 2 giờ hai xe gặp nhau. Hỏi mỗi xe đi cả quãng đường AB trong bao lâu?
Câu hỏi trong đề: Giải SBT Toán 9 CD Bài tập cuối chương 1 có đáp án !!
Quảng cáo
Trả lời:
Gọi x (km/h), y (km/h) lần lượt là tốc độ của xe máy thứ nhất, xe máy thứ hai với x > 0, y > 0.
Theo bài, tốc độ của xe máy thứ hai bằng ![]() tốc độ của xe máy thứ nhất nên ta có phương trình:
tốc độ của xe máy thứ nhất nên ta có phương trình: 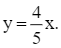
Sau 2 giờ, xe máy thứ nhất đi được quãng đường là: 2x (km) và xe máy thứ hai đi được quãng đường là: 2y (km).
Vì sau 2 giờ hai xe gặp nhau nên ta có:
2x + 2y = AB (trong đó AB là độ dài quãng đường AB).
Ta lập được hệ phương trình: 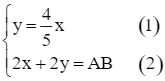
Thế (1) vào phương trình (2), ta nhận được phương trình:
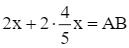
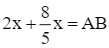
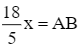
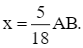
Thay 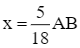 vào phương trình (1), ta được:
vào phương trình (1), ta được:
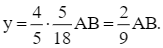
Như vậy, xe máy thứ nhất đi cả quãng đường AB trong: 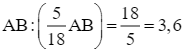 (giờ); xe máy thứ hai đi cả quãng đường AB trong:
(giờ); xe máy thứ hai đi cả quãng đường AB trong: 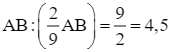 (giờ).
(giờ).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đổi 4 giờ 48 phút = 4,8 giờ.
Gọi x (giờ), y (giờ) lần lượt là thời gian vòi thứ nhất và vòi thứ hai chảy một mình được đầy bể (điều kiện x > 4,8 và y > 4,8).
⦁ Trong 1 giờ, vòi thứ nhất chảy một mình được ![]() (bể), vòi thứ hai chảy một mình được
(bể), vòi thứ hai chảy một mình được ![]() (bể).
(bể).
Hai vòi nước cùng chảy vào một bể sau 4 giờ 48 phút giờ sẽ đầy, nên trong 1 giờ hai vòi cùng chảy thì được 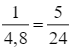 bể, ta có phương trình:
bể, ta có phương trình:
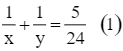
⦁ Trong 4 giờ vòi thứ nhất chảy một mình được ![]() (bể).
(bể).
Trong 3 giờ vòi thứ hai chảy một mình được ![]() (bể).
(bể).
Theo bài, nếu vòi thứ nhất chảy trong 4 giờ, vòi thứ hai chảy trong 3 giờ thì cả hai vòi chảy được ![]() bể nên ta có phương trình:
bể nên ta có phương trình:
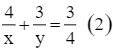
Từ (1) và (2) ta có hệ phương trình: 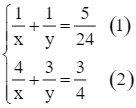
Nhân hai vế của phương trình (1) với 4, ta được hệ phương trình sau:
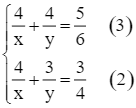
Trừ từng vế của phương trình (3) và (2), ta nhận được phương trình sau:
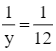 nên y = 12.
nên y = 12.
Thay y = 12 vào phương trình (1), ta được: 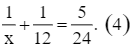
Giải phương trình (4):
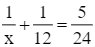
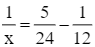
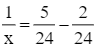
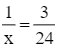
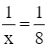
x = 8.
Ta thấy x = 8 và y = 12 thỏa mãn điều kiện.
Vậy thời gian chảy riêng một mình để đầy bể của vòi thứ nhất và vòi thứ hai lần lượt là 8 giờ và 12 giờ.
Lời giải
Gọi x, y (công nhân) lần lượt là số công nhân ở khu công nghiệp A, khu công nghiệp B lúc ban đầu với x, y ∈ ℕ*.
Theo bài, hai khu công nghiệp A và B có tổng cộng 2 200 công nhân nên ta có phương trình: x + y = 2 200. (1)
Khi chuyển 100 công nhân ở khu A sang khu B thì:
⦁ số công nhân ở khu A lúc này là x – 100 (công nhân), do đó ![]() số công nhân ở khu A là
số công nhân ở khu A là 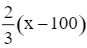 (công nhân).
(công nhân).
⦁ số công nhân ở khu B lúc này là y + 100 (công nhân), do đó ![]() số công nhân ở khu B là
số công nhân ở khu B là 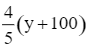 (công nhân).
(công nhân).
Theo bài, sau khi chuyển 100 công nhân ở khu A sang khu B thì ![]() số công nhân ở khu A bằng
số công nhân ở khu A bằng ![]() số công nhân ở khu B nên ta có phương trình:
số công nhân ở khu B nên ta có phương trình:
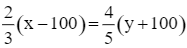
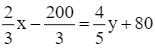
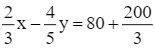
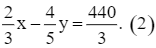
Từ (1) và (2), ta có hệ phương trình: 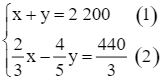
Nhân hai vế của phương trình (1) với 2 và nhân hai vế của phương trình (2) với 3, ta được hệ phương trình sau:
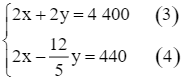
Trừ từng vế hai phương trình (3) và (4), ta nhận được phương trình:
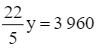 hay y = 900.
hay y = 900.
Thay y = 900 vào phương trình (1) ta có: x + 900 = 2 200 hay x = 1 300.
Ta thấy x = 1 300, y = 900 thỏa mãn điều kiện.
Vậy số công nhân ở khu công nghiệp A và khu công nghiệp B lúc ban đầu lần lượt là 1 300 công nhân và 900 công nhân.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.