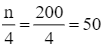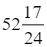Câu hỏi:
13/07/2024 257
Việc kiểm tra chỉ số đường huyết thường xuyên đóng vai trò vô cùng quan trọng để phòng và điều trị bệnh tiểu đường. Khi điều tra chỉ số đường huyết của 100 người cao tuổi ở một địa phương, được kết quả từ 5,0 đến 11,3. Nếu sử dụng mẫu số liệu ghép nhóm để biểu diễn chỉ số đường huyết của 100 người đó thì khoảng biến thiên của mẫu số liệu ghép nhóm đó là bao nhiêu?
A. 5,0.
B. 11,3.
C. 6,3.
D. 100.
Việc kiểm tra chỉ số đường huyết thường xuyên đóng vai trò vô cùng quan trọng để phòng và điều trị bệnh tiểu đường. Khi điều tra chỉ số đường huyết của 100 người cao tuổi ở một địa phương, được kết quả từ 5,0 đến 11,3. Nếu sử dụng mẫu số liệu ghép nhóm để biểu diễn chỉ số đường huyết của 100 người đó thì khoảng biến thiên của mẫu số liệu ghép nhóm đó là bao nhiêu?
A. 5,0.
B. 11,3.
C. 6,3.
D. 100.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: R = 11,3 – 5,0 = 6,3.
Vậy chọn đáp án C.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
a) S |
b) Đ |
c) S |
d) Đ |
Trong mẫu số liệu ghép nhóm trên, ta có: đầu mút trái của nhóm 1 là a1 = 10, đầu mút phải của nhóm 8 là a9 = 90.
Vậy khoảng biến thiên của mẫu số liệu ghép nhóm đó là:
R = a9 – a1 = 90 – 10 = 80 (tuổi).
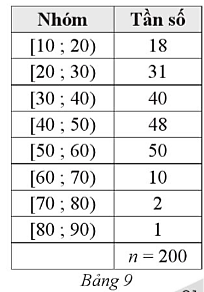
Ta có bảng sau:
Ta có: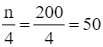 
.
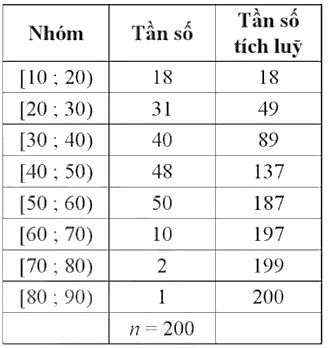
Nhận thấy 49 < 50 < 89 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 50.
Xét nhóm 3 là nhóm [30; 40) có s = 30, h = 10, n3 = 40 và nhóm 2 là nhóm [20; 30) có cf2 = 49.
Ta có: Q1 = s +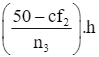 
= 30 + 
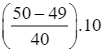= 30,25 (tuổi).
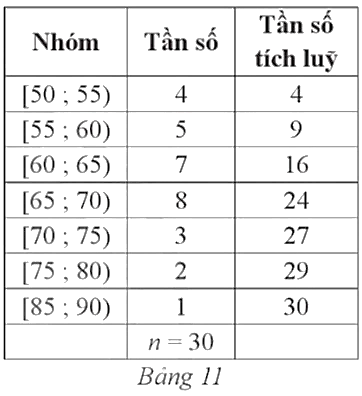
Có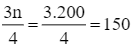 
.
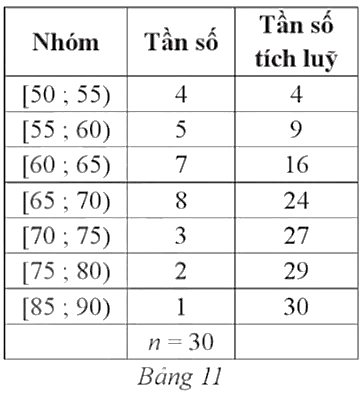
Nhận thấy 137 < 150 < 187 nên nhóm 5 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 150.
Xét nhóm 5 là nhóm [50; 60) có đầu mút trái t = 50, độ dài l = 10, tần số n5 = 50 và nhóm 4 là nhóm [40; 50) có tần số tích lũy cf4 = 137.
Ta có: Q3 = t +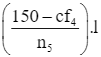 
= 50 + 
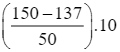= 52,6 (tuổi).
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là:
∆Q = Q3 – Q1 = 52,6 – 30,25 = 22,35 (tuổi).
Lời giải
Đáp án đúng là: A
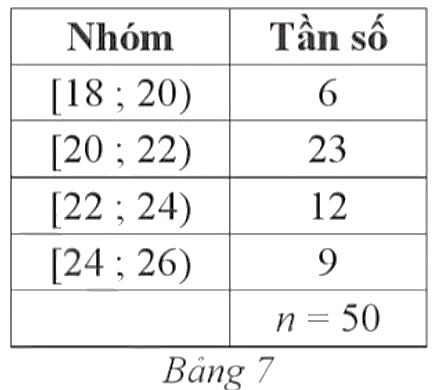
Khoảng tứ phân vị của mẫu số liệu ghép nhóm đó là: ∆Q = Q3 – Q1 = 9 – 4 = 5.
Vậy chọn đáp án A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận