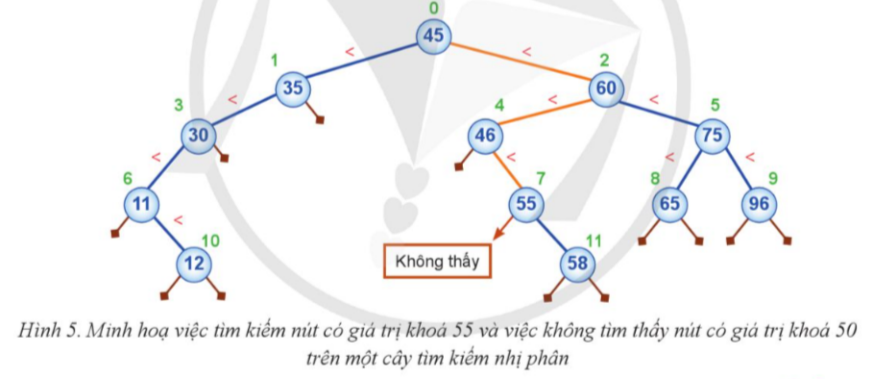
An và Hòa cùng tham gia một hoạt động về bài toán trên dãy số. Giả sử các phần từ 45, 35, 60, 30, 46, 75, 11, 55, 65, 96, 12, 58 của tập số An giữ được biểu diễn dưới dạng cây nhị phân trong Hình 2, các nút được đánh chỉ số từ 0 đến 11. Em hãy quan sát đặc điểm của cây và các giá trị khóa từng nút của cây này, tử đó đưa ra một cách giúp Hoa đạt ít câu hỏi nhất cô thế để tim ra vị trí nút có giá trị khoá 55.
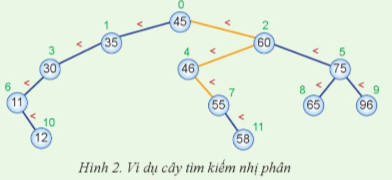
An và Hòa cùng tham gia một hoạt động về bài toán trên dãy số. Giả sử các phần từ 45, 35, 60, 30, 46, 75, 11, 55, 65, 96, 12, 58 của tập số An giữ được biểu diễn dưới dạng cây nhị phân trong Hình 2, các nút được đánh chỉ số từ 0 đến 11. Em hãy quan sát đặc điểm của cây và các giá trị khóa từng nút của cây này, tử đó đưa ra một cách giúp Hoa đạt ít câu hỏi nhất cô thế để tim ra vị trí nút có giá trị khoá 55.

Quảng cáo
Trả lời:
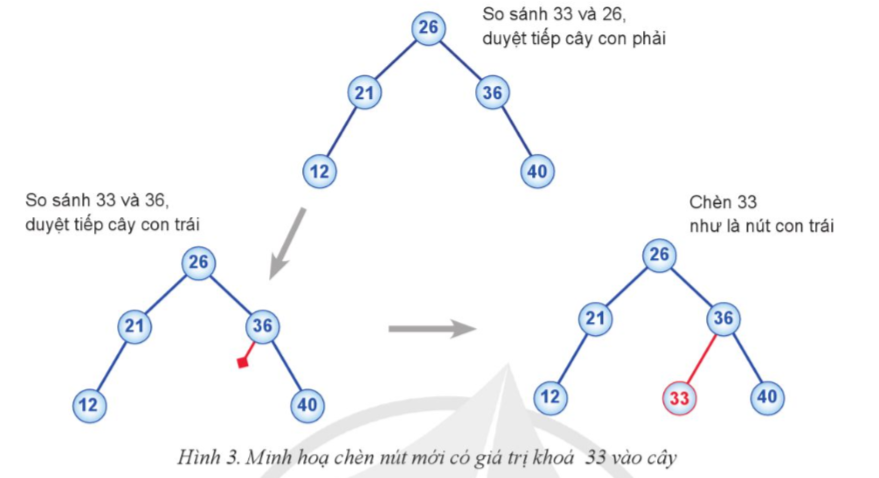
An và Hòa cùng tham gia một hoạt động về bài toán trên dãy số. Giả sử các phần từ 45, 35, 60, 30, 46, 75, 11, 55, 65, 96, 12, 58 của tập số An giữ được biểu diễn dưới dạng cây nhị phân trong Hình 2, các nút được đánh chỉ số từ 0 đến 11. Hướng dẫn các bước xây dựng cây BST từ dãy số [45, 35, 60, 30, 46, 75, 11, 55, 65, 96, 12, 58]:
1. Bắt đầu với 45 là gốc.
2. Chèn 35: 35 < 45, nên 35 là con trái của 45.
3. Chèn 60: 60 > 45, nên 60 là con phải của 45.
4. Chèn 30: 30 < 45 và 30 < 35, nên 30 là con trái của 35.
5. Chèn 46: 46 > 45 và 46 < 60, nên 46 là con trái của 60.
6. Chèn 75: 75 > 45 và 75 > 60, nên 75 là con phải của 60.
7. Chèn 11: 11 < 45 và 11 < 35 và 11 < 30, nên 11 là con trái của 30.
8. Chèn 55: 55 > 45 và 55 < 60 và 55 > 46, nên 55 là con phải của 46.
9. Chèn 65: 65 > 45 và 65 > 60 và 65 < 75, nên 65 là con trái của 75.
10. Chèn 96: 96 > 45 và 96 > 60 và 96 > 75, nên 96 là con phải của 75.
11. Chèn 12: 12 < 45 và 12 < 35 và 12 < 30 và 12 > 11, nên 12 là con phải của 11.
12. Chèn 58: 58 > 45 và 58 < 60 và 58 > 46 và 58 > 55, nên 58 là con phải của 55.
Cây BST sẽ có cấu trúc như sau:
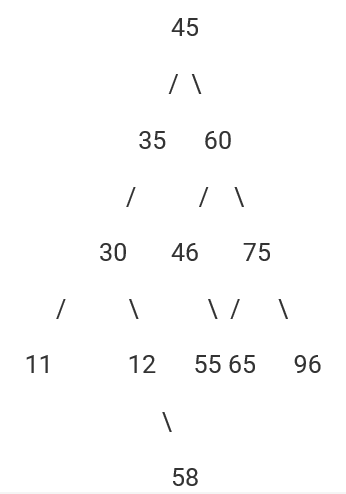
Thực hiện theo các bước sau để tìm giá trị khóa 55,
1. So sánh với nút gốc (45):
o 55 > 45: đi tới cây con phải (60).
2. So sánh với nút 60:
o 55 < 60: đi tới cây con trái (46).
3. So sánh với nút 46:
o 55 > 46: đi tới cây con phải (55).
4. So sánh với nút 55:
o 55 = 55: tìm thấy giá trị khóa.
Vậy, chỉ cần 4 bước so sánh để tìm ra nút có giá trị khóa 55 trong cây này.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sổ tay Hóa học 12 (chương trình mới) ( 18.000₫ )
- Sổ tay dẫn chứng nghị luận xã hội năm 2025 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là c) Cây tìm kiếm nhị phân giúp quá trình tìm kiếm phần tử trong dãy có giá trị cho trước nhanh hơn.
Các câu còn lại sai vì:
a) Sai vì trong cây tìm kiếm nhị phân, giá trị khóa của mọi nút trong cây con trái phải nhỏ hơn giá trị khóa của nút gốc, và giá trị khóa của mọi nút trong cây con phải phải lớn hơn giá trị khóa của nút gốc.
b) Sai vì từ một dãy số nguyên cho trước có thể tạo ra nhiều cây tìm kiếm nhị phân khác nhau tùy thuộc vào thứ tự chèn các số vào cây.
d) Sai vì quá trình tìm kiếm trên cây tìm kiếm nhị phân không luôn luôn cho kết quả tìm được nút có giá trị bằng giá trị khóa cho trước, nó chỉ trả về kết quả nếu giá trị đó thực sự tồn tại trong cây.
Lời giải
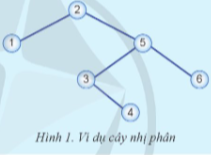
Danh sách giá trị khóa các nút ở cây nhị phân (Hình 1) trong phép duyệt cây theo thứ tự giữa như sau:
1. Bắt đầu từ gốc (2), duyệt cây con trái của 2.
2. Cây con trái của 2 là 1, không có cây con trái và cây con phải. Thăm nút 1.
3. Trở lại nút gốc 2, thăm nút 2.
4. Duyệt cây con phải của 2 là 5.
5. Từ 5, duyệt cây con trái của 5 là 3.
6. Cây con trái của 3 là null, thăm nút 3.
7. Duyệt cây con phải của 3 là 4.
8. Cây con trái và cây con phải của 4 đều là null. Thăm nút 4.
9. Trở lại nút 5, thăm nút 5.
10. Duyệt cây con phải của 5 là 6, không có cây con trái và cây con phải. Thăm nút 6.
Danh sách giá trị khóa các nút theo thứ tự giữa là: 1, 2, 3, 4, 5, 6
Nhận xét đặc điểm của cây nhị phân cùng danh sách được đưa ra:
- Điều này phù hợp với đặc điểm của cây tìm kiếm nhị phân (BST). Trong cây tìm kiếm nhị phân, khi duyệt theo thứ tự giữa, các giá trị khóa luôn được liệt kê theo thứ tự tăng dần.
- Danh sách giá trị khóa được duyệt theo thứ tự giữa (In-order Traversal) của cây nhị phân này là một dãy các giá trị tăng dần.
- Như vậy, cây nhị phân này cũng là một cây tìm kiếm nhị phân.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.