Một túi đựng 24 viên bi giống hệt nhau chỉ khác màu, trong đó có 9 viên bi màu đỏ, 6 viên bi màu xanh, 4 viên bi màu vàng và 5 viên bi màu đen. Bạn An lấy ngẫu nhiên một viên bi từ trong túi.

a) Có bao nhiêu kết quả có thể? Các kết quả có thể này có đồng khả năng không? Tại sao?

b) Tính khả năng để xảy ra mỗi kết quả có thể đó.

c) Tính xác suất để An lấy được:

• viên bi màu đỏ hoặc màu vàng;

• viên bi màu đen hoặc màu xanh;

• viên bi không có màu đen.

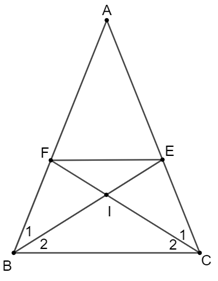
a) Do BE là đường phân giác của góc B nên \({\widehat B_1} = {\widehat B_2},\) ta có: \(\frac{{EA}}{{EC}} = \frac{{BA}}{{BC}}\) (1).

Tương tự với đường phân giác CF, ta có: \(\frac{{FA}}{{FB}} = \frac{{CA}}{{CB}}.\) (2)

Bởi vậy, từ (1) và (2) ta suy ra \(\frac{{EA}}{{EC}} = \frac{{FA}}{{FB}},\) nghĩa là EF định ra trên hai cạnh AB và AC những đoạn thẳng tương ứng tỉ lệ. Do đó theo định lí Thàles đảo ta có EF // BC. Từ đó suy ra ∆BIC ᔕ ∆EIF (ĐPCM).

b) Hai tam giác BFI và CFB có \(\widehat F\) chung, \({\widehat B_1} = \frac{{\widehat {ABC}}}{2} = \frac{{\widehat {ACB}}}{2} = \widehat C{ & _2}.\) Do đó ∆BFI ᔕ ∆CFB suy ra \(\frac{{FB}}{{FC}} = \frac{{FI}}{{FB}}\) hay FB² = FI.FC (ĐPCM).

c) Ta có EF // BC (chứng minh trên).

Do đó \(\frac{{BC}}{{EF}} = \frac{{AB}}{{AF}} = \frac{{\left( {AF + FB} \right)}}{{AF}} = 1 + \frac{{BC}}{{AC}} = 1 + \frac{3}{6} = \frac{3}{2}.\)

Từ đó suy ra \(EF = 3:\frac{3}{2} = 2\) (cm).

Vậy EF = 2 cm.

a) Do O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD nên OA = OC và OB = OD.

Do H và K lần lượt là trung điểm của OB và OD nên \(OH = \frac{{OB}}{2} = \frac{{OD}}{2} = OK.\)

Các kết quả trên cho thấy tứ giác AHCK có hai đường chéo AC và HK cắt nhau tại trung điểm của mỗi đường. Vậy tứ giác AHCK là hình bình hành.

b) • Muốn tứ giác AHCK là hình thoi, ta cần thêm điều kiện hai đường chéo AC và HK vuông góc với nhau, cũng có nghĩa là AC ⊥ BD. Điều này xảy ra khi ABCD là hình thoi. Vậy điều kiện để tứ giác AHCK là hình thoi là: tứ giác ABCD là hình thoi.

• Muốn tứ giác AHCK là hình chữ nhật, ta cần thêm điều kiện hai đường chéo AC và HK bằng nhau, tức là AC = HK. Do H và K lần lượt là trung điểm của OB và OD nên điều kiện đó cũng có nghĩa là \(AC = \frac{1}{2}BD.\) Vậy điều kiện để tứ giác AHCK là hình chữ nhật là: ABCD có đường chéo BD dài gấp 2 lần đường chéo AC.

• Tứ giác AHCK là hình vuông khi nó vừa là hình thoi, vừa là hình chữ nhật. Do đó, theo kết quả hai câu trên, để AHCK là một hình vuông, thì hình bình hành ABCD phải là hình thoi, đường chéo BD dài gấp 2 lần đường chéo AC.