Câu hỏi:
24/07/2024 334
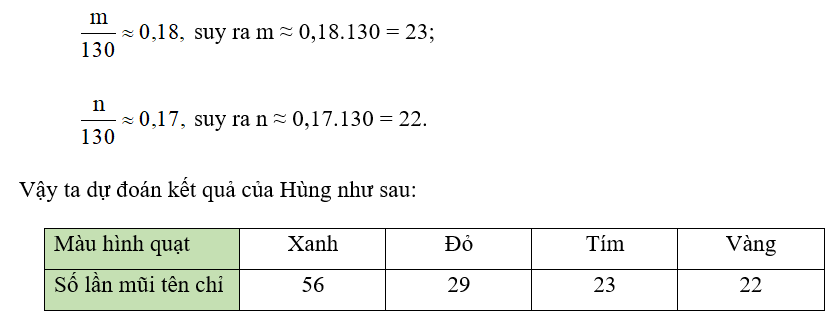
Một hộp đựng 60 viên bi giống hệt nhau gồm ba màu: đỏ, vàng, đen, trong đó có 15 viên bi màu đỏ, 26 viên bi màu vàng. Bỏ thêm 25 viên bi màu đỏ, 14 viên bi màu vàng và lấy ra 10 viên bi màu đen. Chọn ngẫu nhiên một viên bi trong hộp. Tính xác suất để lấy được viên bi:
a) Màu đen;
b) Không phải màu vàng.
Một hộp đựng 60 viên bi giống hệt nhau gồm ba màu: đỏ, vàng, đen, trong đó có 15 viên bi màu đỏ, 26 viên bi màu vàng. Bỏ thêm 25 viên bi màu đỏ, 14 viên bi màu vàng và lấy ra 10 viên bi màu đen. Chọn ngẫu nhiên một viên bi trong hộp. Tính xác suất để lấy được viên bi:
a) Màu đen;
b) Không phải màu vàng.
Câu hỏi trong đề:
Giải VTH Toán 8 KNTT Bài tập cuối chương 8 có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lúc đầu, số viên bi màu đen trong hộp là 60 – 15 – 26 = 19.
Số viên bi trong hộp sau khi bỏ thêm và lấy ra là 60 + 25 + 14 – 10 = 89.
Khi đó, trong hộp có 26 + 14 = 40 viên bi màu vàng và 19 – 10 = 9 viên bi màu đen.
Số viên bi không phải màu vàng là 89 – 40 = 49.
a) Vậy xác suất lấy được viên bi màu đen là
b) Vậy xác suất lấy được viên bi không phải màu vàng là
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một tấm bìa hình tròn được chia thành 4 hình quạt như nhau, tô các màu xanh, đỏ, tím, vàng và được gắn vào trục quay có mũi tên cố định ở tâm. Quay tấm bìa và quan sát xem mũi tên chỉ vào hình quạt nào khi tấm bìa dừng lại. Hai bạn Sơn và Hùng lần lượt thực hiện quay tấm bìa. Bạn Sơn được quay 100 lần và Hùng được quay 130 lần. Sơn quay trước và ghi lại kết quả của mình như sau:
Màu hình quạt
Xanh
Đỏ
Tím
Vàng
Số lần mũi tên chỉ
43
22
18
17
Trước khi Hùng quay, hãy dự đoán xem có bao nhiêu lần mũi tên chỉ vào các hình quạt có màu xanh, đỏ, tím, vàng.
Một tấm bìa hình tròn được chia thành 4 hình quạt như nhau, tô các màu xanh, đỏ, tím, vàng và được gắn vào trục quay có mũi tên cố định ở tâm. Quay tấm bìa và quan sát xem mũi tên chỉ vào hình quạt nào khi tấm bìa dừng lại. Hai bạn Sơn và Hùng lần lượt thực hiện quay tấm bìa. Bạn Sơn được quay 100 lần và Hùng được quay 130 lần. Sơn quay trước và ghi lại kết quả của mình như sau:
|
Màu hình quạt |
Xanh |
Đỏ |
Tím |
Vàng |
|
Số lần mũi tên chỉ |
43 |
22 |
18 |
17 |
Trước khi Hùng quay, hãy dự đoán xem có bao nhiêu lần mũi tên chỉ vào các hình quạt có màu xanh, đỏ, tím, vàng.
Xem đáp án »
24/07/2024
212
Câu 2:
Chọn ngẫu nhiên một số có hai chữ số. Tính xác suất của các biến cố sau:
a) A: “Số được chọn nhỏ hơn 20”;
b) B: “Số được chọn là số chính phương”.
Chọn ngẫu nhiên một số có hai chữ số. Tính xác suất của các biến cố sau:
a) A: “Số được chọn nhỏ hơn 20”;
b) B: “Số được chọn là số chính phương”.
Xem đáp án »
24/07/2024
143
Câu 3:
Một túi đựng các viên bi giống hệt nhau, chỉ khác màu, trong đó có 5 viên bi màu xanh, 3 viên bi màu đỏ và 7 viên bi màu trắng. Bạn Việt lấy ngẫu nhiên một viên bi trong túi. Tính xác suất của các biến cố sau:
a) E: “Việt lấy được viên bi màu xanh”;
b) F: “Việt lấy được viên bi màu đỏ”;
c) G: “Việt lấy được viên bi màu trắng”;
d) H: “Việt lấy được viên bi màu xanh hoặc màu đỏ”;
e) K: “Việt không lấy được viên bi màu đỏ”.
Một túi đựng các viên bi giống hệt nhau, chỉ khác màu, trong đó có 5 viên bi màu xanh, 3 viên bi màu đỏ và 7 viên bi màu trắng. Bạn Việt lấy ngẫu nhiên một viên bi trong túi. Tính xác suất của các biến cố sau:
a) E: “Việt lấy được viên bi màu xanh”;
b) F: “Việt lấy được viên bi màu đỏ”;
c) G: “Việt lấy được viên bi màu trắng”;
d) H: “Việt lấy được viên bi màu xanh hoặc màu đỏ”;
e) K: “Việt không lấy được viên bi màu đỏ”.
Xem đáp án »
24/07/2024
107
Câu 4:
Trong một hộp có 10 tấm thẻ giống nhau được đánh số 11; 12; ...; 20. Rút ngẫu nhiên một tấm thẻ từ trong hộp.
a) Liệt kê các kết quả có thể của hành động trên.
b) Liệt kê các kết quả thuận lợi cho các biến cố sau:
• E: “Rút được tấm thẻ ghi số là bội của 3”;
• F: “Rút được tấm thẻ ghi số nguyên tố”.
Trong một hộp có 10 tấm thẻ giống nhau được đánh số 11; 12; ...; 20. Rút ngẫu nhiên một tấm thẻ từ trong hộp.
a) Liệt kê các kết quả có thể của hành động trên.
b) Liệt kê các kết quả thuận lợi cho các biến cố sau:
• E: “Rút được tấm thẻ ghi số là bội của 3”;
• F: “Rút được tấm thẻ ghi số nguyên tố”.
Xem đáp án »
24/07/2024
95
Câu 5:
Bảng sau đây thống kê kết quả khảo sát số người thích một bộ phim mới tại 5 quận A, B, C, D, E của thành phố X.
|
Quận |
Số người khảo sát |
Số người thích bộ phim mới |
||
|
Nam |
Nữ |
Nam |
Nữ |
|
|
A |
45 |
51 |
10 |
11 |
|
B |
36 |
42 |
9 |
6 |
|
C |
52 |
49 |
13 |
13 |
|
D |
28 |
33 |
9 |
10 |
|
E |
40 |
39 |
7 |
4 |
|
Tổng số |
201 |
214 |
48 |
44 |
a) Chọn ngẫu nhiên một người ở quận C. Ước lượng xác suất của biến cố A: “Người được chọn thích bộ phim đó”.
b) Chọn ngẫu nhiên một người ở quận E. Ước lượng xác suất của biến cố B: “Người được chọn không thích bộ phim đó”.
c) Chọn ngẫu nhiên 600 người ở thành phố X. Ước lượng trong đó có bao nhiêu người thích bộ phim đó.
d) Chọn ngẫu nhiên 500 người nữ ở thành phố X. Ước lượng trong đó có bao nhiêu người thích bộ phim đó.
Xem đáp án »
24/07/2024
69
Câu 6:
Trong một phòng học có 15 học sinh lớp 8A gồm 9 bạn nam, 6 bạn nữ và 15 học sinh lớp 8B gồm 12 bạn nam, 3 bạn nữ. Chọn ngẫu nhiên một học sinh trong phòng. Tính xác suất của các biến cố sau:
a) E: “Chọn được một học sinh nam”;
b) F: “Chọn được một học sinh nam lớp 8B”;
c) G: “Chọn được một học sinh nữ lớp 8A”.
Trong một phòng học có 15 học sinh lớp 8A gồm 9 bạn nam, 6 bạn nữ và 15 học sinh lớp 8B gồm 12 bạn nam, 3 bạn nữ. Chọn ngẫu nhiên một học sinh trong phòng. Tính xác suất của các biến cố sau:
a) E: “Chọn được một học sinh nam”;
b) F: “Chọn được một học sinh nam lớp 8B”;
c) G: “Chọn được một học sinh nữ lớp 8A”.
Xem đáp án »
24/07/2024
61
Bình luận
🔥 Đề thi HOT:
-
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
-
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
-
10 Bài tập Bài toán thực tiễn liên quan đến thể tích, diện tích xung quanh của hình chóp tứ giác đều (có lời giải)
-
Đề kiểm tra Cuối kì 1 Toán 8 KNTT có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 KNTT Bài 1: Đơn thức có đáp án
-
Bài tập Nhân đơn thức với đa thức (có lời giải chi tiết)
-
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
-
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
về câu hỏi!