Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) thỏa mãn \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x + 2m\,,\,\,x \ge 0}\\{{e^x},\,\,x < 0}\end{array}} \right.\) \[(m\] là hằng số). Biết \(\int\limits_{ - 1}^2 {f\left( x \right)dx} = a + \frac{b}{e}\) trong đó \[a,\,\,b\] là các số hữu tỉ. Tính \(a + {b^2}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Do hàm số liên tục trên \(\mathbb{R}\) nên hàm số liên tục tại \(x = 0 \Leftrightarrow \mathop {\lim }\limits_{x \to {0^ - }} f(x) = \mathop {\lim }\limits_{x \to {0^ + }} f(x) = f(0)\)
\( \Leftrightarrow 2m = 1 \Leftrightarrow m = \frac{1}{2}\).
Khi đó, ta có: \(\int\limits_{ - 1}^2 {f\left( x \right)dx} = \int\limits_{ - 1}^0 {f\left( x \right)dx} + \int\limits_0^2 {f\left( x \right)dx} = \int\limits_{ - 1}^0 {{e^x}dx} + \int\limits_0^2 {\left( {x + 1} \right)dx} \)
\( = \left. {{e^x}} \right|_{ - 1}^0 + \left( {\frac{{{x^2}}}{2} + x} \right)_0^2 = 1 - \frac{1}{e} + \frac{4}{2} + 2 = 5 - \frac{1}{e}.\)
Do đó, \(a = 5\,;\,\,b = - 1\). Vậy \(a + {b^2} = 6\). Chọn C.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
![Cho hình chóp có đáy là hình thang \(ABCD\) với \(AD{\rm{ // }}BC\) và \(AD = 2BC\). Gọi \[M\] là điểm trên cạnh \[SD\] thỏa mãn (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid4-1722236954.png)
Gọi \[O\] là giao điểm của \[AC\] và \[BD;{\rm{ }}I\] là giao điểm của \[SO\] và \[BM\,;\,\,N\] là giao điểm của \[AI\] và \[SC\]
Suy ra \[I = \left( {ABM} \right) \cap SC\].
Do \(ABCD\) là hình thang với \(AD{\rm{ // }}BC\) và \(AD = 2BC.\)
\[\frac{{OC}}{{OA}} = \frac{{OB}}{{OD}} = \frac{{BC}}{{AD}} = \frac{1}{2} \Rightarrow \frac{{OA}}{{AC}} = \frac{{OD}}{{BD}} = \frac{2}{3}.\]![Cho hình chóp có đáy là hình thang \(ABCD\) với \(AD{\rm{ // }}BC\) và \(AD = 2BC\). Gọi \[M\] là điểm trên cạnh \[SD\] thỏa mãn (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid6-1722236966.png)
Ta có \(OM{\rm{ // S}}B\) và \[\frac{{OM}}{{SB}} = \frac{2}{3} \Rightarrow \frac{{OI}}{{SI}} = \frac{{OM}}{{SB}} = \frac{2}{3}.\]
Kẻ \(OJ{\rm{ // AN}}\,\,\left( {J \in AN} \right)\)
Xét tam giác \[ANC\] có:
• Vì \(OJ{\rm{ // AN}}\) nên
\[\frac{{OA}}{{AC}} = \frac{2}{3} \Rightarrow \frac{{NJ}}{{NC}} = \frac{2}{3} \Rightarrow \overrightarrow {NJ} = \frac{2}{3}\overrightarrow {NC} .\]• Vì \(IN{\rm{ // OJ}}\) nên \[\frac{{SI}}{{IO}} = \frac{3}{2} \Rightarrow \frac{{SN}}{{NJ}} = \frac{3}{2} \Rightarrow \overrightarrow {SN} = \frac{3}{2}\overrightarrow {NJ} \]\[ \Rightarrow \overrightarrow {SN} = \overrightarrow {NC} \Rightarrow \overrightarrow {SN} = \frac{1}{2}\overrightarrow {SC} \Rightarrow \frac{{SN}}{{SC}} = \frac{1}{2}.\]
Chọn A.
Lời giải
Sơ đồ phản ứng xảy ra như sau:
\({\rm{Al}}{\left( {{\rm{N}}{{\rm{O}}_3}} \right)_3} \cdot 9{{\rm{H}}_2}{\rm{O}} \to {\rm{Al}}{\left( {{\rm{N}}{{\rm{O}}_3}} \right)_3} \to {\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}\)
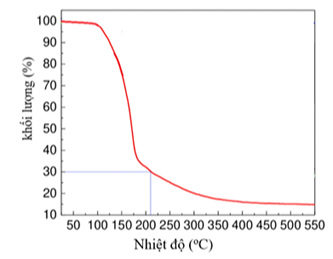
Tại nhiệt độ 210oC, phần rắn còn lại (chứa ba nguyên tố)
=> Hỗn hợp chứa \({\rm{Al}}{\left( {{\rm{N}}{{\rm{O}}_3}} \right)_3}\) và \({\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}\,(3\)nguyên tố là \({\rm{Al,}}\,{\rm{N}},{\rm{O}}).\)
Coi số mol của \({\rm{Al}}{\left( {{\rm{N}}{{\rm{O}}_3}} \right)_3} \cdot 9{{\rm{H}}_2}{\rm{O}} = 1\;{\rm{mol}}\)ta có:
\({\rm{Al}}{\left( {{\rm{N}}{{\rm{O}}_3}} \right)_3}.9{{\rm{H}}_2}{\rm{O}} \to \left\{ {\begin{array}{*{20}{l}}{{\rm{Al}}{{\left( {{\rm{N}}{{\rm{O}}_3}} \right)}_3}:{x^{mol}}}\\{{\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}:{y^{mol}}}\end{array} \Rightarrow {\rm{ }}\left\{ {\begin{array}{*{20}{l}}{x + 2y = 1\,\,({\rm{BTNT}}\,\,{\rm{Al}})}\\{\frac{{213x + 102y}}{{375.1}} \cdot 100\% = 30\% }\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = \frac{{41}}{{108}}}\\{y = \frac{{67}}{{216}}}\end{array}} \right.} \right.} \right.\)
Thành phần % theo khối lượng của oxyen có trong phần chất rắn tại 210oC là
\(\% {m_O} = \frac{{(9x + 3y) \cdot 16}}{{213x + 102y}} \cdot 100\% = 61,83\% .\)
Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo