Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Chuyện chức phán sự đền Tản Viên đề cao tinh thần khảng khái, cương trực, dám đấu tranh chống lại cái ác trừ hại cho dân của Ngô Tử Văn, đồng thời thể hiện niềm tin chân lí, chính nghĩa nhất định thắng gian tà.
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Chuyện chức phán sự đền Tản Viên đề cao tinh thần khảng khái, cương trực, dám đấu tranh chống lại cái ác trừ hại cho dân của Ngô Tử Văn, đồng thời thể hiện niềm tin chân lí, chính nghĩa nhất định thắng gian tà.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chuyện chức phán sự đền Tản Viên đề cao tinh thần khảng khái, cương trực, dám đấu tranh chống lại cái ác trừ hại cho dân của Ngô Tử Văn, đồng thời thể hiện niềm tin công lí, chính nghĩa nhất định thắng gian tà. Chọn C.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
![Cho hình chóp có đáy là hình thang \(ABCD\) với \(AD{\rm{ // }}BC\) và \(AD = 2BC\). Gọi \[M\] là điểm trên cạnh \[SD\] thỏa mãn (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid4-1722236954.png)
Gọi \[O\] là giao điểm của \[AC\] và \[BD;{\rm{ }}I\] là giao điểm của \[SO\] và \[BM\,;\,\,N\] là giao điểm của \[AI\] và \[SC\]
Suy ra \[I = \left( {ABM} \right) \cap SC\].
Do \(ABCD\) là hình thang với \(AD{\rm{ // }}BC\) và \(AD = 2BC.\)
\[\frac{{OC}}{{OA}} = \frac{{OB}}{{OD}} = \frac{{BC}}{{AD}} = \frac{1}{2} \Rightarrow \frac{{OA}}{{AC}} = \frac{{OD}}{{BD}} = \frac{2}{3}.\]![Cho hình chóp có đáy là hình thang \(ABCD\) với \(AD{\rm{ // }}BC\) và \(AD = 2BC\). Gọi \[M\] là điểm trên cạnh \[SD\] thỏa mãn (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid6-1722236966.png)
Ta có \(OM{\rm{ // S}}B\) và \[\frac{{OM}}{{SB}} = \frac{2}{3} \Rightarrow \frac{{OI}}{{SI}} = \frac{{OM}}{{SB}} = \frac{2}{3}.\]
Kẻ \(OJ{\rm{ // AN}}\,\,\left( {J \in AN} \right)\)
Xét tam giác \[ANC\] có:
• Vì \(OJ{\rm{ // AN}}\) nên
\[\frac{{OA}}{{AC}} = \frac{2}{3} \Rightarrow \frac{{NJ}}{{NC}} = \frac{2}{3} \Rightarrow \overrightarrow {NJ} = \frac{2}{3}\overrightarrow {NC} .\]• Vì \(IN{\rm{ // OJ}}\) nên \[\frac{{SI}}{{IO}} = \frac{3}{2} \Rightarrow \frac{{SN}}{{NJ}} = \frac{3}{2} \Rightarrow \overrightarrow {SN} = \frac{3}{2}\overrightarrow {NJ} \]\[ \Rightarrow \overrightarrow {SN} = \overrightarrow {NC} \Rightarrow \overrightarrow {SN} = \frac{1}{2}\overrightarrow {SC} \Rightarrow \frac{{SN}}{{SC}} = \frac{1}{2}.\]
Chọn A.
Lời giải
Sơ đồ phản ứng xảy ra như sau:
\({\rm{Al}}{\left( {{\rm{N}}{{\rm{O}}_3}} \right)_3} \cdot 9{{\rm{H}}_2}{\rm{O}} \to {\rm{Al}}{\left( {{\rm{N}}{{\rm{O}}_3}} \right)_3} \to {\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}\)
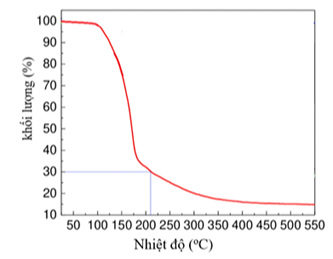
Tại nhiệt độ 210oC, phần rắn còn lại (chứa ba nguyên tố)
=> Hỗn hợp chứa \({\rm{Al}}{\left( {{\rm{N}}{{\rm{O}}_3}} \right)_3}\) và \({\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}\,(3\)nguyên tố là \({\rm{Al,}}\,{\rm{N}},{\rm{O}}).\)
Coi số mol của \({\rm{Al}}{\left( {{\rm{N}}{{\rm{O}}_3}} \right)_3} \cdot 9{{\rm{H}}_2}{\rm{O}} = 1\;{\rm{mol}}\)ta có:
\({\rm{Al}}{\left( {{\rm{N}}{{\rm{O}}_3}} \right)_3}.9{{\rm{H}}_2}{\rm{O}} \to \left\{ {\begin{array}{*{20}{l}}{{\rm{Al}}{{\left( {{\rm{N}}{{\rm{O}}_3}} \right)}_3}:{x^{mol}}}\\{{\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}:{y^{mol}}}\end{array} \Rightarrow {\rm{ }}\left\{ {\begin{array}{*{20}{l}}{x + 2y = 1\,\,({\rm{BTNT}}\,\,{\rm{Al}})}\\{\frac{{213x + 102y}}{{375.1}} \cdot 100\% = 30\% }\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = \frac{{41}}{{108}}}\\{y = \frac{{67}}{{216}}}\end{array}} \right.} \right.} \right.\)
Thành phần % theo khối lượng của oxyen có trong phần chất rắn tại 210oC là
\(\% {m_O} = \frac{{(9x + 3y) \cdot 16}}{{213x + 102y}} \cdot 100\% = 61,83\% .\)
Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo