Câu hỏi:
30/07/2024 95
Cho hình hộp đứng \(ABCD.A'B'C'D'\) có đáy \({\rm{ABCD}}\) là một hình thoi cạnh \({\rm{a}},\) \(\widehat {{\rm{ABC}}} = 120^\circ ,\)\({\rm{A}}A' = 4{\rm{a}}\). Biết \({\rm{a}} = 4\), tính khoảng cách giữa hai đường thẳng \(A'{\rm{C}}\) và \({\rm{B}}B'.\)
Đáp án: ……….
Cho hình hộp đứng \(ABCD.A'B'C'D'\) có đáy \({\rm{ABCD}}\) là một hình thoi cạnh \({\rm{a}},\) \(\widehat {{\rm{ABC}}} = 120^\circ ,\)\({\rm{A}}A' = 4{\rm{a}}\). Biết \({\rm{a}} = 4\), tính khoảng cách giữa hai đường thẳng \(A'{\rm{C}}\) và \({\rm{B}}B'.\)
Đáp án: ……….
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa... kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 70k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
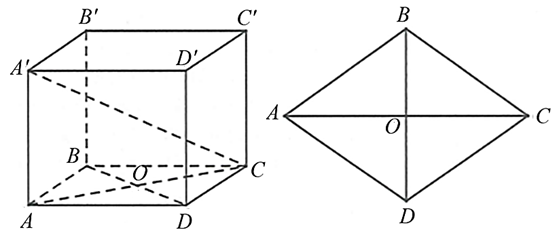
Ta có\(\left( {A'{\rm{AC}}} \right)\)là mặt phẳng chứa \(A'{\rm{C}}\) và song song với \({\rm{B}}B' \Rightarrow {\rm{d}}\left( {{\rm{B}}B',A'{\rm{C}}} \right) = {\rm{d}}\left( {{\rm{B}},\,\left( {{\rm{A}}A'{\rm{C}}} \right)} \right)\).
Gọi \(O\) là tâm hình thoi \(ABCD \Rightarrow BO \bot AC\).
Do \(ABCD.A'B'C'D'\) là hình hộp đứng nên \(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot BO\).
\(\left\{ {\begin{array}{*{20}{l}}{BO \bot AC}\\{BO \bot AA'}\end{array} \Rightarrow BO \bot \left( {AA'C} \right) \Rightarrow d\left( {B,\,\,\left( {AA'C} \right)} \right) = BO} \right.\).
Hình thoi \({\rm{ABCD}}\) có \(\widehat {{\rm{ABC}}} = 120^\circ \Rightarrow {\rm{ABC}}\) là tam giác đều \( \Rightarrow {\rm{BD}} = {\rm{AB}} = {\rm{a}} \Rightarrow {\rm{BO}} = \frac{{\rm{a}}}{2}\).
Vậy \(d\left( {BB',A'C} \right) = d\left( {B,\left( {AA'C} \right)} \right) = BO = \frac{a}{2} = \frac{4}{2} = 2\). Đáp án: 2.
Nhà sách VIETJACK:
Sách Combo - Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) - 2024 cho 2k7 VietJack
Đã bán 1,4k
₫ 290.000
₫ 140.000
Sách - Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) cho 2k7 VietJack
Đã bán 902
₫ 150.000
₫ 39.000
Sách - Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) cho 2k7 VietJack
Đã bán 851
₫ 150.000
₫ 39.000
Sách Combo - Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) - 2024 cho 2k7 VietJack
Đã bán 1,4k
₫ 280.000
₫ 150.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Dựa vào các tiêu chí chủ yếu nào sau đây để phân chia thế giới thành các nhóm nước?
Xem đáp án »
30/07/2024
10,660
Câu 2:
Đất đai ở các đồng bằng miền Đông Trung Quốc khá màu mở do nguyên nhân chủ yếu nào sau đây?
Xem đáp án »
30/07/2024
2,445
Câu 3:
Cho phương trình \(2\sin x - \sqrt 3 = 0\). Tổng các nghiệm thuộc \(\left[ {0\,;\,\,\pi } \right]\) của phương trình là
Xem đáp án »
30/07/2024
2,294
Câu 4:
So với các vùng lãnh thổ khác của nước ta, Duyên hải Nam Trung Bộ có
Xem đáp án »
30/07/2024
2,291
Câu 5:
Thế mạnh về tự nhiên nào sau đây là quan trọng nhất để phát triển khai thác thủy sản ở Duyên hải Nam Trung Bộ?
Xem đáp án »
30/07/2024
1,729
Câu 6:
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức \(F\left( x \right) = \frac{1}{{40}}{x^2}\left( {30 - x} \right)\), trong đó \(x\) là liều lượng thuốc tiêm cho bệnh nhân (\(x\) được tính bằng miligam) và \(x \in \left[ {0\,;\,\,30} \right].\)Hãy tìm liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất.
Đáp án: ……….
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức \(F\left( x \right) = \frac{1}{{40}}{x^2}\left( {30 - x} \right)\), trong đó \(x\) là liều lượng thuốc tiêm cho bệnh nhân (\(x\) được tính bằng miligam) và \(x \in \left[ {0\,;\,\,30} \right].\)Hãy tìm liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất.
Đáp án: ……….
Xem đáp án »
30/07/2024
1,575
Câu 7:
Bảng 1 dưới dây thống kế số lượng và thời gian sử dụng hàng ngày của các thiết bị điện của một gia đình trong tháng 1 năm 2024. Bảng 2 cho biết thang giá điện sinh hoạt hiện nay.
Bảng 1
Bảng 2
Thiết bị
Công suất
(W)
Số lượng
(cái)
Thời gian sử dụng trong ngày
Bóng đèn
25
3
5h
Tivi
60
1
4h
Tủ lạnh
75
1
24h
Máy bơm
120
1
30ph
Ấm điện
500
1
15ph
Nồi cơm
600
1
1h
Bậc
Điện năng tiêu thụ
(kWh)
Giá tiền cho 1 kWh
1
0 – 50
1484 đồng
2
51 – 100
1533 đồng
3
101 – 200
1786 đồng
Tính số tiền điện gia đình này cần phải trả?
Đáp án: ……….
Bảng 1 dưới dây thống kế số lượng và thời gian sử dụng hàng ngày của các thiết bị điện của một gia đình trong tháng 1 năm 2024. Bảng 2 cho biết thang giá điện sinh hoạt hiện nay.
|
Bảng 1 |
Bảng 2 |
||||||||||||||||||||||||||||||||||||||||
|
|
Tính số tiền điện gia đình này cần phải trả?
Đáp án: ……….
Xem đáp án »
30/07/2024
1,435
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 2)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 13)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận