Câu hỏi:
31/07/2024 136
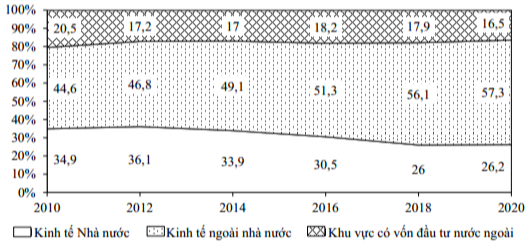
Cho hàm số \(y = f\left( x \right)\), hàm số \(y = f'\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Bất phương trình \(f\left( x \right) < m - {x^3} - x\) (\(m\) là tham số thực) nghiệm đúng với mọi \(x \in \left( { - 2\,;\,\,0} \right)\) khi và chỉ khi
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có: \(f\left( x \right) < m - {x^3} - x\)\( \Leftrightarrow f\left( x \right) + {x^3} + x < m,\,{\mkern 1mu} {\mkern 1mu} \forall x \in \left( { - 2\,;\,\,0} \right)\).
Đặt \(g\left( x \right) = f\left( x \right) + {x^3} + x\) ta có \(g\left( x \right) < m{\mkern 1mu} {\mkern 1mu} \forall x \in \left( { - 2;0} \right)\)\( \Leftrightarrow m \ge \mathop {\max }\limits_{\left[ { - 2;0} \right]} g\left( x \right)\).
Ta có: \(g'\left( x \right) = f'\left( x \right) + 3{x^2} + 1\); \(g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = - 3{x^2} - 1\).
Số nghiệm của phương trình \(g'\left( x \right) = 0\) là số giao điểm của đồ thị hàm số \(y = f'\left( x \right)\) và đồ thị hàm số \(y = - 3{x^2} - 1\).
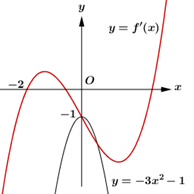
Dựa vào đồ thị hàm số ta thấy trên \(\left[ { - 2\,;\,\,0} \right]\), phương trình \(g'\left( x \right) = 0\) có duy nhất nghiệm \(x = 0\).
Ta có bảng biến thiên hàm số \(y = g\left( x \right)\):
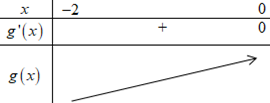
Dựa vào bảng biến thiên ta thấy: \(\mathop {\max }\limits_{\left[ { - 2\,;\,\,0} \right]} g\left( x \right) = g\left( 0 \right) = f\left( 0 \right)\).
Vậy \(m \ge f\left( 0 \right)\). Chọn D.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đoạn thơ đã thể hiện lòng yêu mến, thái độ trân trọng của tác giả đối với vẻ đẹp và sự giàu có, phong phú của tiếng Việt. Tác giả đã so sánh tiếng Việt với những hình ảnh thiên nhiên quen thuộc như “đất cày, lụa, tre ngà, tơ” để biểu đạt sự gắn bó với quê hương và sự mềm mại, óng ánh của tiếng Việt. Tác giả cũng đã miêu tả tiếng Việt như tiếng nói vẹn tròn từ trước khi có chữ viết, như tiếng hát tha thiết kể mọi điều bằng ríu rít âm thanh, như gió nước không thể nắm bắt để biểu đạt sự cổ xưa, giàu cảm xúc và phong phú của tiếng Việt. Tác giả cũng đã nhắc đến những dấu huyền, dấu ngã để biểu đạt sự đặc trưng và khó nắm bắt của tiếng Việt. Chọn D.
Lời giải
Tỉ trọng thành phần kinh tế ngoài Nhà nước lớn nhất và có xu hướng tăng. → xu hướng giảm, tỉ trọng nhỏ hơn ngoài Nhà nước. Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 3)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận