Một người đầu tư cùng một số tiền vào hai lĩnh vực A và B. Nhà đầu tư này ghi lại số tiền thu được hàng tháng trong hai năm theo mỗi lĩnh vực cho kết quả như sau:

Tính độ lệch chuẩn của hai mẫu số liệu ghép nhóm và nhận xét về mức độ ổn định của số tiền thu được hàng tháng khi đầu tư vào hai lĩnh vực trên.
Một người đầu tư cùng một số tiền vào hai lĩnh vực A và B. Nhà đầu tư này ghi lại số tiền thu được hàng tháng trong hai năm theo mỗi lĩnh vực cho kết quả như sau:

Tính độ lệch chuẩn của hai mẫu số liệu ghép nhóm và nhận xét về mức độ ổn định của số tiền thu được hàng tháng khi đầu tư vào hai lĩnh vực trên.
Quảng cáo
Trả lời:
Chọn giá trị đại diện cho các nhóm số liệu ta có bảng thống kê sau:
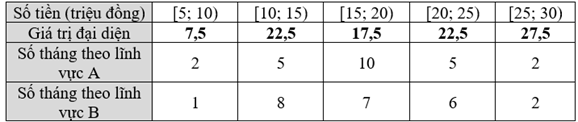
Cỡ mẫu của lĩnh vực A là: nA = 2 + 5 + 10 + 5 + 2 = 24.
Cỡ mẫu của lĩnh vực B là: nB = 1 + 8 + 7 + 6 + 2 = 24.
Số tiền trung bình thu được mỗi tháng từ lĩnh vực A là:
\({\overline x _A}\) = \(\frac{1}{{24}}\)(2.7,5 + 5.22,5 + 10.17,5 + 5.22,5 + 2.27,5) = 17,5.
Số tiền trung bình thu được mỗi tháng từ lĩnh vực B là:
\({\overline x _B}\) = \(\frac{1}{{24}}\)(1.7,5 + 8.22,5 + 7.17,5 + 6.22,5 + 2.27,5) = 17,5.
Độ lệch chuẩn của số tiền thu được trong các tháng theo lĩnh vực A là:
sA = \(\sqrt {\frac{1}{{24}}\left( {2.7,{5^2} + 5.12,{5^2} + 10.17,{5^2} + 5.22,{5^2} + 2.27,{5^2}} \right) - 17,{5^2}} \) ≈ 5,2.
Độ lệch chuẩn của số tiền thu được trong các tháng theo lĩnh vực A là:
sB = \(\sqrt {\frac{1}{{24}}\left( {1.7,{5^2} + 8.12,{5^2} + 7.17,{5^2} + 6.22,{5^2} + 2.27,{5^2}} \right) - 17,{5^2}} \) ≈ 5,2.
Do các độ lệch chuẩn sA = sB ≈ 5,2 nên mức độ ổn định của hai phương án đầu tư là như nhau.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Chọn giá trị đại diện cho các nhóm số liệu ta có bảng thống kê sau:
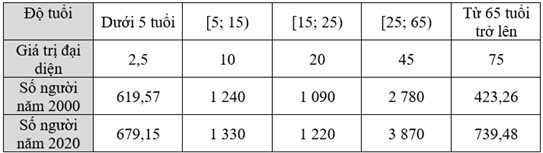
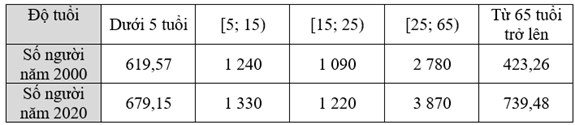
Ước lượng tuổi trung bình của dân số thế giới năm 2000 là:
\({\overline x _{2000}}\) = \(\frac{{2,5.619,57 + 10.1240 + 20.1090 + 45.2780 + 75.423,26}}{{619,57 + 1240 + 1090 + 2780 + 423,26}}\) ≈ 31,3016.
Ước lượng tuổi trung bình của dân số thế giới năm 2020 là:
\({\overline x _{2020}}\) = \(\frac{{2,5.679,15 + 10.1330 + 20.1220 + 45.3870 + 75.739,48}}{{679,15 + 1330 + 1220 + 3870 + 739,48}}\) ≈ 34,3184.
b) Với mẫu số liệu về tuổi của dân số thế giới năm 2000:
Cỡ mẫu là: 619,57 + 1240 + 1090 + 2780 + 423,26 = 6152,83.
Do \(\frac{n}{4} = \frac{{6152,83}}{4}\)= 1538,2075 nên nhóm chứa tứ phân vị thứ nhất là [5; 15). Ta có:
Q1 = 5 + \(\frac{{1538,2075 - 619,57}}{{1240}}.10\) ≈ 12,41.
Do \(\frac{{3n}}{4} = \frac{{3.6152,83}}{4}\) = 4614,6225 nên nhóm chứa tứ phân vị thứ ba là [25; 65). Ta có:
Q3 = 25 + \(\frac{{4614,6225 - (619,57 + 1240 + 1090)}}{{2780}}.40\) ≈ 48,96.
Như vậy, khoảng tứ phân vị của mẫu số liệu về tuổi dân số thế giới năm 2000 là:
∆Q2000 ≈ 48,96 – 12,41 = 36,55.
Với mẫu số liệu về tuổi của dân số thế giới năm 2020:
Cỡ mẫu là: 679,15 + 1330 + 1220 + 3870 + 739,48 = 7838,63.
Do \(\frac{n}{4} = \frac{{7838,63}}{4}\) = 1959,6575 nên nhóm chứa tứ phân vị thứ nhất là [5; 15). Ta có:
Q1 = 5 + \(\frac{{1959,6575 - 679,15}}{{1330}}.10\) ≈ 14,63.
Do \(\frac{{3n}}{4} = \frac{{3.1959,6575}}{4}\) = 5878,9725 nên nhóm chứa tứ phân vị thứ ba là [25; 65). Ta có:
Q3 = 25 + \(\frac{{5878,9725 - (679,15 + 1330 + 1220)}}{{3870}}.40\) ≈ 52,39.
Như vậy, khoảng tứ phân vị của mẫu số liệu về tuổi dân số thế giới năm 2020 là:
∆Q2020 ≈ 52,39 – 14,63 = 37,76.
Nhận xét: Dân số thế giới năm 2020 già hơn và có độ tuổi phân tán hơn so với dân số thế giới năm 2000.
Lời giải
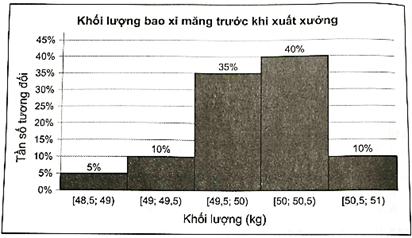
Khoảng biến thiên của mẫu số liệu trên là: R = 4 – 2,5 = 1,5.
Cỡ mẫu là n = 20 + 30 + 40 + 35 + 25 = 150.
Do \(\frac{n}{4} = \frac{{150}}{4}\) = 37,5 nên nhóm chứa tứ phân vị thứ nhất là [2,8; 3,1). Ta có:
Q1 = 2,8 + \(\frac{{37,5 - 20}}{{30}}.0,3\) = 2,975.
Do \(\frac{{3n}}{4} = \frac{{3.150}}{4}\)= 112,5 nên nhóm chứa tứ phân vị thứ ba là [3,4; 3,7). Ta có:
Q3 = 3,4 + \(\frac{{112,5 - \left( {20 + 30 + 40} \right)}}{{35}}.0,3\) ≈ 3,593.
Do đó, khoảng tứ phân vị là ∆Q ≈ 3,593 – 2,975 = 0,618.
Các giá trị này cho ta biết về độ phân tán của mẫu số liệu ghép nhóm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.