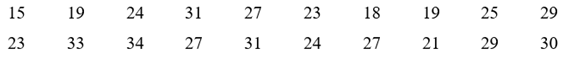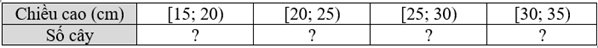Giải SBT Toán 12 Tập 1 KNTT Bài 10. Phương sai và độ lệch chuẩn có đáp án

Chọn giá trị đại diện cho mỗi nhóm dố liệu ta có mẫu số liệu sau:

Cỡ mẫu là: 5 + 12 + 15 + 3 = 35.

Số trung bình là:

\(\overrightarrow x \) = \(\frac{1}{{35}}\)(5.6,75 + 12.7,25 + 15.7,75 + 3.8,35) ≈ 7,48.

Độ lệch chuẩn là:

s = \(\sqrt {\frac{1}{{35}}\left( {5.6,{{75}^2} + ... + 3.8,{{25}^2}} \right) - 7,{{48}^2}} \) ≈ 0,39.

a) Tổng chiều cao 20 cây xoan giống đó là:

15 + 19 + 24 + 31 + 27 + 23 + 18 + 19 + 25 + 29 + 23 + 33 + 34 + 27 + 31 + 24 + 27

+ 21 + 29 + 30 = 509.

Chiều cao trung bình của 20 cây xoan giống là: \(\frac{{509}}{{20}}\) = 25,45.

Ta có: Tổng bình phương của 20 giá trị số liệu trong bảng là:

15² + 19² + 24² + 31² + 27² + 23² + 18² + 19² + 25² + 29² + 23² + 33² + 34² + 27² + 31²

+ 24² + 27² + 21² + 29² + 30² = 13 483.

Lúc này, độ lệch chuẩn của mẫu số liệu gốc là:

S_g = \(\sqrt {\frac{1}{{20}}.13483 - 25,{{45}^2}} \) ≈ 5,14.

b) Ta có bảng số liệu ghép nhóm như sau:

Ta có bảng giá trị đại diện là:

Số trung bình là:

\(\overline x \) = \(\frac{{4.17,5 + 5.22,5 + 6.27,5 + 5.32,5}}{{20}}\) = 25,5.

Độ lệch chuẩn là:

s = \(\sqrt {\frac{1}{{20}}\left( {4.17,{5^2} + 5.22,{5^2} + 6.27,{5^2} + 5.32,{5^2}} \right) - 25,{5^2}} \) ≈ 5,34.

c) Từ số liệu tính được phần a, b ta nên dùng giá trị s_g để đo mức độ phân tán về chiều cao của 20 cây xoan giống.

a) Độ lệch chuẩn của mẫu số liệu ghép nhóm về thành tích 20 lần luyện tập (đơn vị tính là phút) của một vận động viên chạy cự li 1 000 m cho biết mức độ ổn định trong thành tích của vận động viên này.

b) Độ lệch chuẩn của mẫu số liệu ghép nhóm về kết quả 20 lần đo khoảng cách từ Trái Đất đến một ngôi sao (đơn vị là năm ánh sáng) khi dùng một thiết bị đo mới được chế tạo cho biết độ chính xác của thiết bị này. Độ lệch chuẩn càng nhỏ thì thiết bị đo càng chính xác.

Chọn giá trị đại diện cho mỗi nhóm ta có bảng số liệu sau:

Doanh thu trung bình một tháng của cửa hàng trong năm 2022 là:

\(\overline x  = \frac{1}{{12}}\)(17,5.1 + 5.22,5 + 4.27,5 + 2.32,5) ≈ 25,42.

Doanh thu trung bình một tháng của cửa hàng trong năm 2023 là:

\(\overline x  = \frac{1}{{12}}\)(3.17,5 + 4.22,5 + 3.27,5 + 2.32,5) ≈ 24,17.

Độ lệch chuẩn cho doanh thu các tháng năm 2022 là:

S₂₀₂₂ = \(\sqrt {\frac{1}{{12}}\left( {17,{5^2} + 5.22,{5^2} + 4.27,{5^2} + 2.32,{5^2}} \right) - 25,{{42}^2}} \) ≈ 4,29.

Độ lệch chuẩn cho doanh thu các tháng năm 2023 là:

S₂₀₂₃ = \(\sqrt {\frac{1}{{12}}\left( {3.17,{5^2} + 4.22,{5^2} + 3.27,{5^2} + 2.32,{5^2}} \right) - 24,{{17}^2}} \) ≈ 5,12.

Do đó s₂₀₂₂ < s₂₀₂₃.

Như vậy, doanh thu hằng tháng của cửa hàng trong năm 2022 ổn định hơn.

Chọn giá trị đại diện cho bảng số liệu, ta có bảng sau:

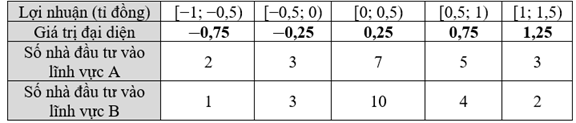
Lợi nhuận trung bình của các nhà đầu tư vào lĩnh vực A là:

\(\overline x  = \frac{1}{{20}}\left[ {2.\left( { - 0,75} \right) + 3.\left( { - 0,25} \right) + 7.0,25 + 5.0,75 + 3.1,25} \right]\) = 0,35.

Lợi nhuận trung bình của các nhà đầu tư vào lĩnh vực B là:

\(\overline x  = \frac{1}{{20}}\left[ {1.\left( { - 0,75} \right) + 3.\left( { - 0,25} \right) + 10.0,25 + 4.0,75 + 2.1,25} \right]\) = 0,325.

Độ lệch chuẩn của lợi nhuận khi đầu tư vào lĩnh vực A là:

s_A = \(\sqrt {\frac{1}{{20}}\left[ {2.{{\left( { - 0,75} \right)}^2} + 3.{{\left( { - 0,25} \right)}^2} + 7.0,{{25}^2} + 5.0,{{75}^2} + 3.1,{{25}^2}} \right] - 0,{{35}^2}} \) ≈ 0,58.

Độ lệch chuẩn của lợi nhuận khi đầu tư vào lĩnh vực B là:

s_B = \(\sqrt {\frac{1}{{20}}\left[ {1.{{\left( { - 0,75} \right)}^2} + 3.{{\left( { - 0,25} \right)}^2} + 10.0,{{25}^2} + 4.0,{{75}^2} + 2.1,{{25}^2}} \right] - 0,{{35}^2}} \)≈ 0,48.

Do s_A > s_B nên đầu tư vào lĩnh vực A rủi ro hơn lĩnh vực B.