Giải SBT Toán 12 Tập 1 KNTT Bài 5. Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn có đáp án
55 người thi tuần này 4.6 1.2 K lượt thi 10 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Lời giải
Gọi x, y (m) lần lượt là chiều dài hai cạnh của thửa ruộng hình chữ nhật. Giả sự cạnh giáp sông của thửa ruộng có độ dài là y (m).
Khi đó, theo đề bài ta có: 2x + y = 240 hay y = 240 – 2x.
Do đó: 0 < x < 120; y > 0.
Diện tích cửa thửa ruộng là
S = xy = x(240 – 2x) = 240x – 2x2, 0 < x < 120.
Ta có: S' = 240 – 4x
S' = 0 ⇔ x = 60 (vì 0 < x < 120).
Khi đó y = 240 – 2.60 = 120.
Lập bảng biến thiên:
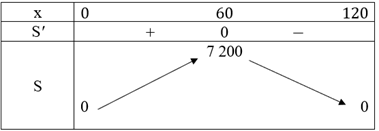
Vậy thửa ruộng có diện tích lớn nhất là:
S = 60. 120 = 7 200 (m2) (khi cạnh giáp sông và cạnh đối diện có độ dài 120 m, hai cạnh kia có độ dài 60 m).
Chú ý: Nếu phải rào cả bốn cạnh cửa thửa ruộng thì dễ thấy thửa ruộng có diện tích lớn nhất khi nó là hình vuông, tức là bốn cạnh đều dài 60 m, và khi đó diện tích lớn nhất là
3 600 m2.
Lời giải
Ta có: R'(x) = \(\frac{{5000}}{{1 + 5{e^{ - x}}}}\), x ≥ 0.
R''(x) = \(\frac{{ - 25000{e^{ - x}}{{\left( {1 + 5{e^{ - x}}} \right)}^2} + 25000{e^{ - x}}.2\left( {1 + 5{e^{ - x}}} \right).5{e^{ - x}}}}{{{{\left( {1 + 5{e^{ - x}}} \right)}^4}}}\)
R''(x) = 0 ⇔ x = ln5 ≈ 1,61.
Ta có bảng biến thiên như sau:
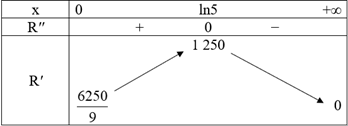
Từ bảng biến thiên, ta thấy tốc độ bán hàng đạt tối đa vào thời điểm năm thứ hai.
Lời giải
Gọi x (m) là cạnh đáy của chiếc hộp.
Khi đó, ta có chiều cao của chiếc hộp là \(\frac{{2000}}{{{x^2}}}\) (cm).
Suy ra, tổng diện tích bề mặt của chiếc hộp là:
S = 2x2 + 4x.\(\frac{{2000}}{{{x^2}}}\) = 2x2 + \(\frac{{8000}}{x}\), x > 0.
Ta có: S' = 4x – \(\frac{{8000}}{{{x^2}}}\) = \(\frac{{4{x^3} - 8000}}{{{x^2}}}\)
S' = 0 ⇔ x = 10\(\sqrt[3]{2}\).
Ta có bảng biến thiên:
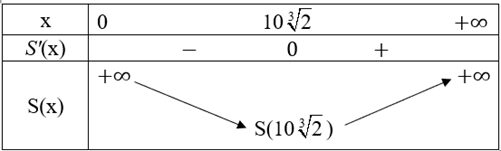
Dễ thấy lượng vật liệu dùng để sản xuất là nhỏ nhất khi cạnh đáy của hộp là 10\(\sqrt[3]{2}\) (cm) và chiều cao của hộp là \(\frac{{20}}{{\sqrt[3]{4}}}\) cm.
Lời giải
Gọi khoảng cách từ thị trấn đến chỗ neo thuyền leo x (km), khi đó 0 ≤ x ≤ 12.
Từ đề bài, ta có khoảng cách từ hòn đảo đến nơi neo thuyền là: (12 – x)2 + 9 (km).
Thời gian để người đó từ hòn đảo đến thị trấn là: T = \(\frac{{{{\left( {12 - x} \right)}^2} + 9}}{{2,5}} + \frac{x}{4}\) (giờ).
Ta có: T' = \( - \frac{{2\left( {12 - x} \right)}}{{2,5}} + \frac{1}{4}\)
T' = 0 ⇔ x = \(\frac{{187}}{{16}}\) = 11,6875.
Mặt khác, ta có T(0) = 61,2; T(11,6875) ≈ 6,56; T(12) = 6,6.
Vậy người đó cần neo thuyền tại vị trí cách thị trấn 11,6875 km để thời gian đi lại là gần nhất.
Lời giải
Gọi bán kính đáy của thùng hình trụ là r. Suy ra, chiều cao của thùng hình trụ là \(\frac{V}{{\pi {r^2}}}\).
Diện tích bề mặt của thùng hình trụ là S = 2πr2 + \(\frac{{2\pi rV}}{{\pi {r^2}}}\) = 2πr2 + \(\frac{{2V}}{r}\), r > 0.
Ta có: S' = 2πr2 – \(\frac{{2V}}{{{r^2}}}\) = \(\frac{{4\pi {r^3} - 2V}}{{{r^2}}}\)
S' = 0 ⇔ r = \(\sqrt[3]{{\frac{V}{{2\pi }}}}\).
Bảng biến thiên của hàm số:
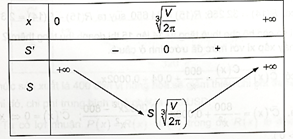
Từ bảng biến thiên: S đạt giá trị nhỏ nhất khi r = \(\sqrt[3]{{\frac{V}{{2\pi }}}}\), khi đó chiều cao của hình trụ là
2.\(\sqrt[3]{{\frac{V}{{2\pi }}}}\) = 2r.
Đây là điều cần chứng minh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
