Giải SBT Toán 12 Tập 1 KNTT Bài 1. Tính đơn điệu và cực trị của hàm số có đáp án
54 người thi tuần này 4.6 1 K lượt thi 9 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Lời giải
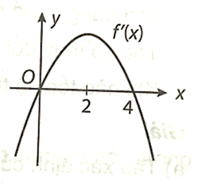
a) Quan sát đồ thị, ta có:
f'(x) < 0 trên các khoảng (−∞; 0) và (4; +∞) nên hàm số f(x) nghịch biến trên các khoảng (−∞; 0) và (4; +∞).
f'(x) > 0 trên khoảng (0; 4) nên hàm số f(x) đồng biến trên khoảng (0; 4).
b) Vì f'(x) đổi dấu từ dương sang âm khi x đi qua giá trị x = 4 nên hàm số f(x) nên hàm số đạt cực đại tại x = 4.
Vì f'(x) đổi dấu từ âm sang dương khi x đi qua giá trị x = 0 nên hàm số f(x) nên hàm số đạt cực tiểu tại x = 0.
Lời giải
a) y = x3 – 9x2 – 48x + 52
Tập xác định: D = ℝ.
y' = 0 ⇔ 3x2 – 18x – 48 = 0 ⇔ x = 8 hoặc x = −2.
Ta có bảng biến thiên như sau:
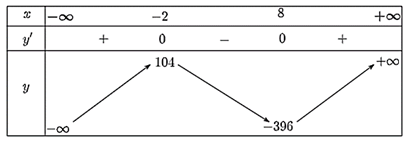
Từ bảng biến thiên, ta có:
Hàm số đồng biến trên các khoảng (−∞; −2) và (8; +∞).
Hàm số nghịch biến trên khoảng (−2; 8).
Hàm số đạt cực đại tại x = −2 và yCĐ = y(−2) = 104.
Hàm số đạt cực tiểu tại x = 8 và yCT = y(8) = −396.
b) y = −x3 + 6x2 + 9
Tập xác định: D = ℝ.
Ta có: y' = −3x2 + 12x
y' = 0 ⇔ −3x2 + 12x = 0 ⇔ x = 0 hoặc x = 4.
Ta có bảng biến thiên như sau:
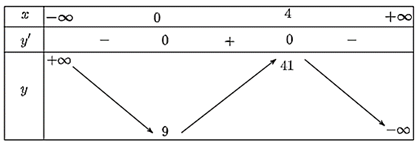
Từ bảng biến thiên, ta có:
Hàm số đồng biến trên khoảng (0; 4).
Hàm số nghịch biến trên các khoảng (−∞; 0) và (4; +∞).
Hàm số đạt cực đại tại x = 4 và yCĐ = y(4) = 41.
Hàm số đạt cực tiểu tại x = 0 và yCT = y(0) = 9.
Lời giải
a) \(y = x + \frac{1}{x}\)
Tập xác định: D = ℝ\{0}.
Ta có: y' = 1 – \(\frac{1}{{{x^2}}}\) = \(\frac{{{x^2} - 1}}{{{x^2}}}\)
y' = 0 ⇔ \(\frac{{{x^2} - 1}}{{{x^2}}}\) = 0 ⇔ x = ±1.
Ta có bảng biến thiên:
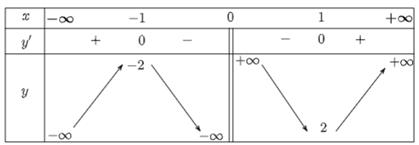
Từ bảng biến thiên, ta có:
Hàm số nghịch biến trên các khoảng (−1; 0) và (0; 1).
Hàm số đồng biến trên các khoảng (−∞; −1) và (1; +∞).
Hàm số đạt cực đại tại x = −1 và yCĐ = y(−1) = −2.
Hàm số đạt cực tiểu tại x = 1 và yCT = y(1) = 2.
b) \(y = \frac{x}{{{x^2} + 1}}.\)
Tập xác định: D = ℝ.
Ta có: y' = \(\frac{{1 - {x^2}}}{{{{\left( {{x^2} + 1} \right)}^2}}}\)
y' = 0 ⇔ \(\frac{{1 - {x^2}}}{{{{\left( {{x^2} + 1} \right)}^2}}}\) = 0 ⇔ 1 – x2 = 0 ⇔ x = ±1.
Ta có bảng biến thiên như sau:
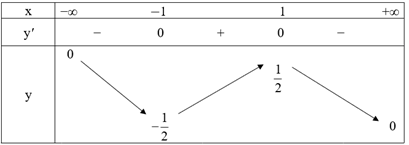
Từ bảng biến thiên, ta có:
Hàm số nghịch biến trên các khoảng (−∞; −1) và (1; +∞).
Hàm số đồng biến trên khoảng (−1; 1).
Hàm số đạt cực đại tại x = 1 và yCĐ = y(1) = \(\frac{1}{2}\).
Hàm số đạt cực tiểu tại x = −1 và yCT = y(−1) = \( - \frac{1}{2}\).
Lời giải
a) y = x4 – 2x2 + 3
Tập xác định: D = ℝ.
Ta có: y' = 4x3 – 4x
y' = 0 ⇔ 4x3 – 4x = 0 ⇔ x = 0 hoặc x = ±1.
Ta có bảng biến thiên như sau:
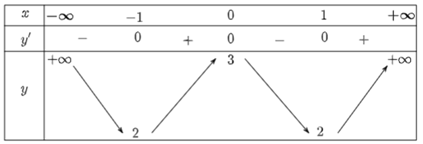
Từ bảng biến thiên, ta có:
Hàm số nghịch biến trên các khoảng (−∞; −1) và (0; 1).
Hàm số đồng biến trên các khoảng (−1; 0) và (1; +∞).
Hàm số đạt cực đại tại x = 0 và yCĐ = y(0) = 3.
Hàm số đạt cực tiểu tại x = 1 và tại x = −1 và yCT = y(1) = y(−1) = 2.
b) y = x2lnx
Tập xác định: D = (0; +∞).
Ta có: y' = 2xlnx + x = x(2lnx + 1)
y' = 0 ⇔ x(2lnx + 1) = 0 ⇔ x = \({e^{ - \frac{1}{2}}}\).
Từ đây ta có bảng biến thiên như sau:
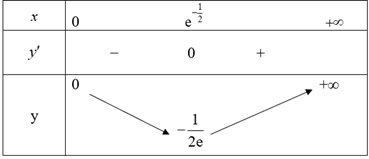
Hàm số nghịch biến trên khoảng \(\left( {0;{e^{ - \frac{1}{2}}}} \right)\).
Hàm số đồng biến trên khoảng \(\left( {{e^{ - \frac{1}{2}}}; + \infty } \right)\).
Hàm số đạt cực tiểu tại x = \({e^{ - \frac{1}{2}}}\) và yCT = y\(\left( {{e^{ - \frac{1}{2}}}} \right)\) = \( - \frac{1}{{2e}}\).
Lời giải
Xét \(\mathop {\lim }\limits_{x \to {0^ - }} \frac{{f(x) - f(0)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sqrt[3]{{{x^2}}}}}{x} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{1}{{\sqrt[3]{x}}} = - \infty .\)
\(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f(x) - f(0)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{\sqrt[3]{{{x^2}}}}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{\sqrt[3]{x}}} = + \infty .\)
Như vậy, hàm số \(f(x) = \sqrt[3]{{{x^2}}}\) không có đạo hàm tại x = 0.
Với mọi x ≠ 0, f(x) > 0 = f(0) nên hàm số f(x) đạt cực tiểu tại x = 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.