Hàm chi phí và hàm doanh thu (đều tính bằng triệu đồng) của một loại sản phẩm lần lượt là C(x) = 25,5x + 1 000 và R(x) = 75,5x, trong đó x là số đơn vị sản phẩm đó được sản xuất và bán ra.
a) Tính hàm lợi nhuận trung bình \(\overline P (x) = \frac{{R(x) - C(x)}}{x}\).
b) Tìm lợi nhuận trung bình khi mức sản xuất x lần lượt là 100, 500 và 1 000 đơn vị sản phẩm.
c) Xét tính đơn điệu của hàm lợi nhuận trung bình \(\overline P (x)\) trên khoảng (0; +∞) và tính giới hạn của hàm số này khi x → +∞. Giải thích ý nghĩa thực tiễn của kết quả nhận được.
Hàm chi phí và hàm doanh thu (đều tính bằng triệu đồng) của một loại sản phẩm lần lượt là C(x) = 25,5x + 1 000 và R(x) = 75,5x, trong đó x là số đơn vị sản phẩm đó được sản xuất và bán ra.
a) Tính hàm lợi nhuận trung bình \(\overline P (x) = \frac{{R(x) - C(x)}}{x}\).
b) Tìm lợi nhuận trung bình khi mức sản xuất x lần lượt là 100, 500 và 1 000 đơn vị sản phẩm.
c) Xét tính đơn điệu của hàm lợi nhuận trung bình \(\overline P (x)\) trên khoảng (0; +∞) và tính giới hạn của hàm số này khi x → +∞. Giải thích ý nghĩa thực tiễn của kết quả nhận được.
Quảng cáo
Trả lời:
a) Ta có: \(\overline P (x) = \frac{{R(x) - C(x)}}{x} = \frac{{75,5x - 25,5x - 1000}}{x} = 50 - \frac{{1000}}{x}\) (triệu đồng).
Tập xác định của hàm lợi nhuận trung bình là: (0; +∞).
b) Với x = 100 thì \(\overline P (100) = 50 - \frac{{1000}}{{100}} = 40\) (triệu đồng).
Với x = 500 thì \(\overline P (500) = 50 - \frac{{1000}}{{500}} = 48\) (triệu đồng).
Với x = 1 000 thì \(\overline P (1000) = 50 - \frac{{1000}}{{1000}} = 49\) (triệu đồng).
c) Ta có: \(\overline P (x) = 50 - \frac{{1000}}{x}\)
\(\overline {P'} \left( x \right) = \frac{{1000}}{{{x^2}}}\)> 0 với mọi x ∈ (0; +∞).
Vậy hàm lợi nhuận trung bình đồng biến trên khoảng (0; +∞).
Mặt khác, \(\mathop {\lim }\limits_{x \to + \infty } \overline P (x) = \mathop {\lim }\limits_{x \to + \infty } \left( {50 - \frac{{1000}}{x}} \right) = 50.\)
Ta có bảng biến thiên như sau:
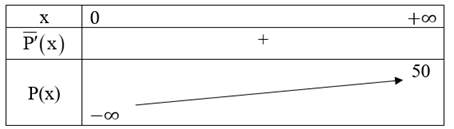
Như vậy, mặc dù lợi nhuận trung bình luôn tăng khi mức sản xuất tăng nhưng không vượt quá 50 triệu đồng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có: \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{4} = \frac{\pi }{2}.\)
Khi đó, vị trí của vật tại thời điểm t là x(t) = 0,24cos\(\frac{{\pi t}}{2}\) (m).
Suy ra vị trí của vật tại thời điểm t = 0,5 giây là x(0,5) = 0,24cos\(\frac{{0,5\pi }}{2}\) = \(0,12\sqrt 2 \) (m).
b) Vận tốc của vật là v(t) = x'(t) = −0,12sin\(\frac{{\pi t}}{2}\) (m/s).
Tại thời điểm t = 0,5 giây thì v(0,5) = −0,12sin\(\frac{{0,5\pi }}{2}\) = −0,06π\(\sqrt 2 \) (m/s).
Dấu âm của vận tốc chứng tỏ tại thời điểm này, vật đang chuyển động theo chiều ngược với chiều dương của trục đã chọn.
c) Gia tốc của vật là: a(t) = v'(t) = −0,06π2cos\(\frac{{\pi t}}{2}\) (m/s2).
d) Tại thời điểm t = 0,5 giây, ta có lực tác động lên vật là:
F(0,5) = m.a(0,5) = −0,06π2cos\(\frac{{0,5\pi }}{2}\) = −0,03π\(\sqrt 2 \) (N).
Vậy độ lớn của lực tác dụng lên vật là 0,03π\(\sqrt 2 \) N và lực có hướng ngược với chiều dương của trục đã chọn.
e) Vị trí của vật tại thời điểm ban đầu t = 0 là x(0) = 0,24 (m).
Ta có: x(t) = 0,24cos\(\frac{{\pi t}}{2}\) = −0,12 ⇔ cos\(\frac{{\pi t}}{2}\) = \( - \frac{1}{2}\)
Nghiệm t dương nhỏ nhất của phương trình trên là t = \(\frac{4}{3}\).
Vậy thời gian tối thiểu để vật chuyển động từ vị trí ban đầu đến vị trí x = −0,12 m là
t = \(\frac{4}{3}\) giây.
Khi đó, vận tốc của vật là \(v\left( {\frac{4}{3}} \right)\) = −0,12πsin\(\frac{{\pi \frac{4}{3}}}{2}\) = −0,06π\(\sqrt 3 \) (m/s).
Lời giải
a) Ta có: x(t) = t3 – 7t2 + 11t + 5 với t ∈ [0; 5].
Vận tốc của vật là v(t) = x'(t) = 3t2 – 14t + 11, t ∈ [0; 5].
v(t) = 0 ⇔ 3t2 – 14t + 11 = 0 ⇔ t = 1 hoặc t = \(\frac{{11}}{3}\).
Ta có bảng biến thiên như sau:
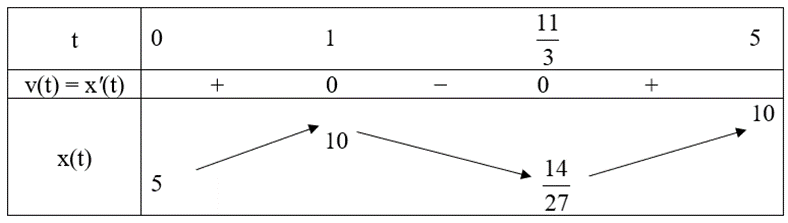
Dựa vào bảng trên, v(t) > 0 khi t ∈ (0; 1) hoặc \(\left( {\frac{{11}}{3};5} \right)\); v(t) < 0 khi t ∈ \(\left( {1;\frac{{11}}{3}} \right)\).
Vật chuyển động theo chiều dương khi vận tốc v(t) > 0.
Do đó, vật chuyển động sang phải trong các khoảng thời điểm từ 0 đến 1 giây và từ \(\frac{{11}}{3}\) giây đến 5 giây; vật chuyển động sang trái trong các khoảng thời gian từ 1 giây đến \(\frac{{11}}{3}\) giây.
b) Tốc độ của vật là độ lớn của vận tốc, tức là:
\[\left| {v\left( t \right)} \right| = \left| {3{t^2}--14t + 11} \right|\], t ∈ [0; 5].
Ta có \[\left| {v\left( t \right)} \right|\] = 0 ⇔ t = 1 hoặc t = \(\frac{{11}}{3}\).
Vậy vật dừng lại tại các thời điểm t = 1 giây hoặc t = \(\frac{{11}}{3}\) giây.
Ta có: v(t) = 3t2 – 14t + 11, t ∈ [0; 5].
v'(t) = 6t – 14, t ∈ [0; 5].
v'(t) = 0 ⇔ 6t – 14 = 0 ⇔ t = \(\frac{7}{3}.\)
Xét trên đoạn [1; 4], ta có: v(1) = 0, v(4) = −5, v\(\left( {\frac{7}{3}} \right) = \frac{{ - 16}}{3}\).
Vì \[\left| {v\left( 1 \right)} \right|{\rm{ }} < {\rm{ }}\left| {v\left( 4 \right)} \right|{\rm{ }} < {\rm{ }}\left| {v\left( {\frac{7}{3}} \right)} \right|\] do đó\(\mathop {\max }\limits_{t \in [1;4]} \left| {v(t)} \right| = \left| {v\left( {\frac{7}{3}} \right)} \right| = \frac{{16}}{3}\).
Vậy tốc độ cực đại của vật trong khoảng thời gian từ t = 1 giây đến t = 4 giây là \(\frac{{16}}{3}\) (m/s).
c) Gia tốc của vật là: a(t) = v'(t) = 6t – 14.
Ta có bảng biến thiên sau:
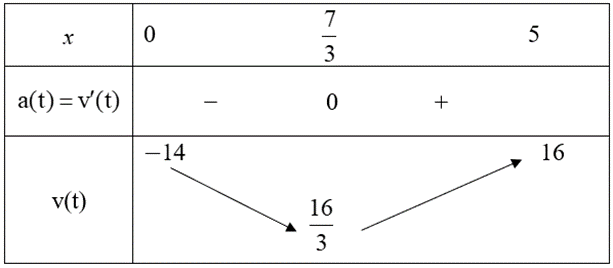
Từ đây, a(t) > 0 khi t ∈ \(\left( {\frac{7}{3};5} \right)\) và a(t) < 0 khi t ∈ \(\left( {0;\frac{7}{3}} \right)\).
Vật tăng tốc khi a(t) > 0 và vật giảm tốc khi a(t) < 0. Vậy vật tăng tốc trong khoảng thời gian từ \(\frac{7}{3}\)giây đến 5 giây và vật giảm tốc trong khoảng thời gian từ 0 giây đến \(\frac{7}{3}\) giây.Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.