Giải SGK Toán 12 KNTT Bài 19. Công thức xác suất toàn phần và công thức Bayes có đáp án
58 người thi tuần này 4.6 1.3 K lượt thi 13 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
a) Với A là biến cố “Trời mưa” và B là biến cố “Bán hết vé”.
Theo bài ra ta có: P(A) = 0,75. Suy ra P() = 1 – P(A) = 1 – 0,75 = 0,25.
Lại có:
+) nếu trời mưa thì xác suất bán hết vé là 0,4. Vậy P(B | A) = 0,4.
+) nếu trời không mưa thì xác suất bán hết vé là 0,9. Vậy = 0,9.
b) Nhà tổ chức quan tâm tới P(B) nhất.
Lời giải
Gọi A là biến cố: “Trời mưa” và B là biến cố: “Bán hết vé”.
Từ HĐ 1a, ta có: P(A) = 0,75; P() = 1 – P(A) = 0,25;
P(B | A) = 0,4; = 0,9.
Thay vào công thức xác suất toàn phần ta được
P(B) = P(A) ∙ P(B | A) + P() ∙ = 0,75 ∙ 0,4 + 0,25 ∙ 0,9 = 0,525.
Vậy xác suất để nhà tổ chức sự kiện bán hết vé là 0,525.
Lời giải
Kí hiệu A là biến cố: “Thứ Ba, ông An đi làm bằng xe máy”; B là biến cố: “Thứ Tư, ông An đi làm bằng xe máy”.
Khi đó, biến cố “Thứ Tư, ông An đi làm bằng xe buýt” chính là .
Ta có sơ đồ hình cây mô tả xác suất của biến cố như sau:
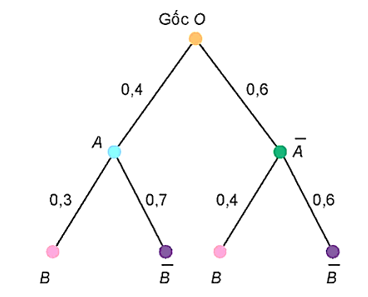
Hai nhánh cây đi tới là và .
Như vậy = 0,4 ∙ 0,7 + 0,6 ∙ 0,6 = 0,64.
Lời giải
Gọi A là biến cố: “Cây bố có kiểu gene bb”;
M là biến cố: “Cây con lấy gene b từ cây bố”;
N là biến cố: “Cây con lấy gene b từ cây mẹ”;
E là biến cố: “Cây con có kiểu gene bb”.
Theo giả thiết, M và N độc lập nên P(E) = P(M) ∙ P(N).
Tính P(M): Ta áp dụng công thức xác suất toàn phần:
P(M) = P(A) ∙ P(M | A) + P() ∙ P(M | ). (*)
Ta có P(A) = 0,4; P() = 0,6.
P(M | A) là xác suất để cây con lấy gene b từ cây bố với điều kiện cây bố có kiểu gene bb. Do đó, P(M | A) = 1.
P(M | ) là xác suất để cây con lấy gene b từ cây bố với điều kiện cây bố có kiểu gene Bb. Do đó, P(M | ) = 0,5.
Thay vào (*) ta được: P(M) = 0,4 ∙ 1 + 0,6 ∙ 0,5 = 0,7.
Tương tự tính được P(N) = 0,7.
Vậy P(E) = P(M) ∙ P(N) = 0,7 ∙ 0,7 = 0,49.
Từ kết quả trên suy ra trong một quần thể các cây đậu Hà Lan, mà ở đó tỉ lệ cây bố và cây mẹ mang kiểu gene bb, Bb tương ứng là 40% và 60%, thì tỉ lệ cây con có kiểu gene bb là khoảng 49%.
Lời giải
a) Gọi A là biến cố: “Cây bố có kiểu gene bb”;
K là biến cố: “Cây con nhận gene B từ bố”;
H là biến cố: “Cây con nhận gene B từ mẹ”;
F là biến cố: “Cây con có kiểu gene BB”.
Theo giả thiết, K và H độc lập nên P(F) = P(K) ∙ P(H).
Ta tính P(K) theo công thức xác suất toàn phần:
P(K) = P(A) ∙ P(K | A) + P() ∙ P(K | ). (1)
Ta có P(A) = 0,4; P() = 0,6.
P(K | A) là xác suất để cây con nhận gene B từ bố với điều kiện bố có kiểu gene bb.
Vậy P(K | A) = 0.
P(K | ) là xác suất để cây con nhận gene B từ bố với điều kiện bố có kiểu gene Bb.
Vậy P(K | ) = 0,5.
Thay vào (2) ta được P(K) = 0,4 ∙ 0 + 0,6 ∙ 0,5 = 0,3.
Tương tự tính được P(H) = 0,3.
Vậy P(F) = P(K) ∙ P(H) = 0,3 ∙ 0,3 = 0,09.
Vậy tỉ lệ cây con có kiểu gene BB là khoảng 9%.
b) Gọi G là biến cố: “Cây con có kiểu gene Bb”.
Vì và hai biến cố E, F xung khắc nên
P() = P(E) + P(F) = 0,49 + 0,09 = 0,58.
Vậy P(G) = 1 – P() = 1 – 0,58 = 0,42.
Vậy tỉ lệ cây con có kiểu gene Bb là khoảng 42%.
Câu 6
Tình huống mở đầu
Trong Y học, để chẩn đoán bệnh X nào đó, người ta thường dùng một xét nghiệm. Xét nghiệm dương tính, tức là xét nghiệm đó kết luận một người mắc bệnh X. Xét nghiệm âm tính, tức là xét nghiệm đó kết luận một người không mắc bệnh X. Vì không có một xét nghiệm nào tuyệt đối đúng nên trên thực tế có thể xảy ra hai sai lầm sau:
– Xét nghiệm dương tính nhưng thực tế người xét nghiệm không mắc bệnh. Ta gọi đây là dương tính giả.
– Xét nghiệm âm tính nhưng thực tế người xét nghiệm lại mắc bệnh. Ta gọi đây là âm tính giả.
Ông M đi xét nghiệm bệnh hiểm nghèo X. Biết rằng, nếu một người mắc bệnh X thì với xác suất 0,95 xét nghiệm cho dương tính; nếu một người không bị bệnh X thì với xác suất 0,01 xét nghiệm cho dương tính.
Xét nghiệm của ông M cho kết quả dương tính. Ông M hoảng hốt khi nghĩ rằng mình có xác suất 0,95 mắc bệnh hiểm nghèo X.
Trong tình huống mở đầu Mục 2, gọi A là biến cố: “Ông M mắc bệnh hiểm nghèo X”; B là biến cố: “Xét nghiệm cho kết quả dương tính”.
a) Nêu các nội dung còn thiếu tương ứng với “(?)” để hoàn thành các câu sau đây:
P(A | B) là xác suất để (?) với điều kiện (?);
P(B | A) là xác suất để (?) với điều kiện (?).
b) 0,95 là P(A | B) hay P(B | A)? Có phải ông M có xác suất 0,95 mắc bệnh hiểm nghèo X không?
Tình huống mở đầu
Trong Y học, để chẩn đoán bệnh X nào đó, người ta thường dùng một xét nghiệm. Xét nghiệm dương tính, tức là xét nghiệm đó kết luận một người mắc bệnh X. Xét nghiệm âm tính, tức là xét nghiệm đó kết luận một người không mắc bệnh X. Vì không có một xét nghiệm nào tuyệt đối đúng nên trên thực tế có thể xảy ra hai sai lầm sau:
– Xét nghiệm dương tính nhưng thực tế người xét nghiệm không mắc bệnh. Ta gọi đây là dương tính giả.
– Xét nghiệm âm tính nhưng thực tế người xét nghiệm lại mắc bệnh. Ta gọi đây là âm tính giả.
Ông M đi xét nghiệm bệnh hiểm nghèo X. Biết rằng, nếu một người mắc bệnh X thì với xác suất 0,95 xét nghiệm cho dương tính; nếu một người không bị bệnh X thì với xác suất 0,01 xét nghiệm cho dương tính.
Xét nghiệm của ông M cho kết quả dương tính. Ông M hoảng hốt khi nghĩ rằng mình có xác suất 0,95 mắc bệnh hiểm nghèo X.
Trong tình huống mở đầu Mục 2, gọi A là biến cố: “Ông M mắc bệnh hiểm nghèo X”; B là biến cố: “Xét nghiệm cho kết quả dương tính”.
a) Nêu các nội dung còn thiếu tương ứng với “(?)” để hoàn thành các câu sau đây:
P(A | B) là xác suất để (?) với điều kiện (?);
P(B | A) là xác suất để (?) với điều kiện (?).
b) 0,95 là P(A | B) hay P(B | A)? Có phải ông M có xác suất 0,95 mắc bệnh hiểm nghèo X không?
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.