Giải SGK Toán 12 KNTT Bài 13. Ứng dụng hình học của tích phân có đáp án

30 người thi tuần này 4.6 1 K lượt thi 15 câu hỏi

Câu 1/15

Xét hình phẳng giới hạn bởi đường thẳng y = f(x) = x + 1, trục hoành và hai đường thẳng x = −2; x = 1 (H.4.12).

a) Tính diện tích S của hình phẳng này.

b) Tính $\int_{- 2}^{1} |f (x)| d x$ và so sánh với S.

Xem đáp án

Lời giải

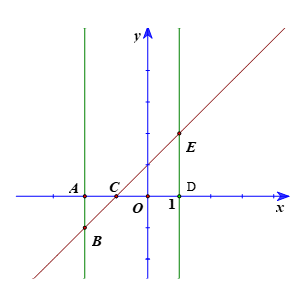
Xét hình phẳng giới hạn bởi đường thẳng y = f(x) = x + 1, trục hoành và hai đường thẳng (ảnh 2)

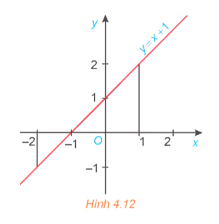
Gọi A(−2; 0), C(−1; 0), D(1; 0) và B, E lần lượt là giao điểm của đường thẳng x = −2, x = 1 với đường thẳng y = x + 1.

Do đó B(−2; −1), E(1; 2).

Khi đó S = S_∆ABC + S_∆CDE = $\frac{1}{2}AB.AC + \frac{1}{2}CD.DE$$ = \frac{1}{2}.1.1 + \frac{1}{2}.2.2 = \frac{5}{2}$.

b) $\int\limits_{ - 2}^1 {\left| {f\left( x \right)} \right|} dx$$ = \int\limits_{ - 2}^1 {\left| {x + 1} \right|} dx$$ = \int\limits_{ - 2}^{ - 1} {\left| {x + 1} \right|} dx + \int\limits_{ - 1}^1 {\left| {x + 1} \right|} dx$$ = - \int\limits_{ - 2}^{ - 1} {\left( {x + 1} \right)} dx + \int\limits_{ - 1}^1 {\left( {x + 1} \right)} dx$

\[ = - \left. {\left( {\frac{{{x^2}}}{2} + x} \right)} \right|_{ - 2}^{ - 1} + \left. {\left( {\frac{{{x^2}}}{2} + x} \right)} \right|_{ - 1}^1\]\[ = \frac{1}{2} + \frac{3}{2} + \frac{1}{2} = \frac{5}{2}\].

Vậy $S = \int\limits_{ - 2}^1 {\left| {f\left( x \right)} \right|} dx$.

Câu 2/15

Tính diện tích hình phẳng giới hạn bởi parabol y = x² – 4, trục hoành và hai đường thẳng x = 0; x = 3 (H.4.15).

Xem đáp án

Lời giải

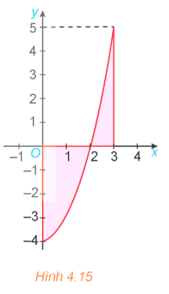
Diện tích hình phẳng cần tính là:

$\int\limits_0^3 {\left| {{x^2} - 4} \right|} dx$$ = \int\limits_0^2 {\left| {{x^2} - 4} \right|} dx + \int\limits_2^3 {\left| {{x^2} - 4} \right|} dx$$ = \int\limits_0^2 {\left( {4 - {x^2}} \right)} dx + \int\limits_2^3 {\left( {{x^2} - 4} \right)} dx$

$ = \left. {\left( {4x - \frac{{{x^3}}}{3}} \right)} \right|_0^2 + \left. {\left( {\frac{{{x^3}}}{3} - 4x} \right)} \right|_2^3$$ = \frac{{16}}{3} - 3 + \frac{{16}}{3} = \frac{{23}}{3}$.

Câu 3/15

Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của các hàm số f(x) = −x² + 4x, g(x) = x và hai đường thẳng x = 1, x = 3 (H.4.16).

a) Giả sử S₁ là diện tích hình phẳng giới hạn bởi parabol y = −x² + 4x, trục hoành và hai đường thẳng x = 1, x = 3; S₂ là diện tích hình phẳng giới hạn bởi đường thẳng y = x, trục hoành và hai đường thẳng x = 1, x = 3. Tính S₁, S₂ và từ đó suy ra S.

b) Tính $\int_{1}^{3} |f (x) - g (x)| d x$ và so sánh với S.

Xem đáp án

Lời giải

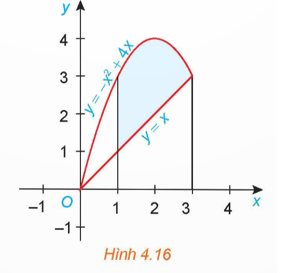
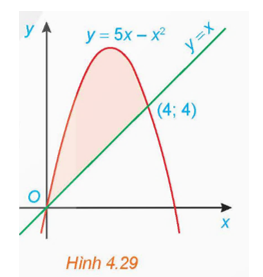
a) Ta có ${S_1} = \int\limits_1^3 {\left| { - {x^2} + 4x} \right|dx} $$ = \int\limits_1^3 {\left( { - {x^2} + 4x} \right)dx} $$ = \left. {\left( { - \frac{{{x^3}}}{3} + 2{x^2}} \right)} \right|_1^3$$ = 9 - \frac{5}{3} = \frac{{22}}{3}$.

${S_2} = \int\limits_1^3 {\left| x \right|} dx$$ = \int\limits_1^3 x dx$$ = \left. {\frac{{{x^2}}}{2}} \right|_1^3 = \frac{9}{2} - \frac{1}{2} = 4$.

Do đó S = S₁ – S₂ = $\frac{{22}}{3} - 4 = \frac{{10}}{3}$.

b) $\int\limits_1^3 {\left| {f\left( x \right) - g\left( x \right)} \right|} dx$$ = \int\limits_1^3 {\left| { - {x^2} + 4x - x} \right|} dx$$ = \int\limits_1^3 {\left| { - {x^2} + 3x} \right|} dx$$ = \int\limits_1^3 {\left( { - {x^2} + 3x} \right)} dx$

$ = \left. {\left( { - \frac{{{x^3}}}{3} + 3.\frac{{{x^2}}}{2}} \right)} \right|_1^3$$ = \frac{9}{2} - \frac{7}{6} = \frac{{10}}{3}$.

Vậy $S = \int\limits_1^3 {\left| {f\left( x \right) - g\left( x \right)} \right|} dx$.

Câu 4/15

Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số $y = \sqrt{x}$ , y = x – 2 và hai đường thẳng x = 1, x = 4.

Xem đáp án

Lời giải

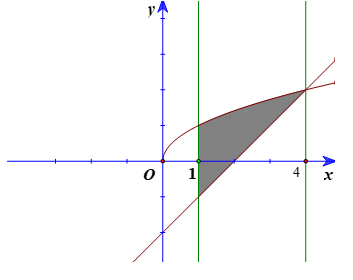
Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số y = căn x , y = x – 2 và hai đường thẳng x = 1, x = 4. (ảnh 1)

Diện tích hình phẳng cần tính là:

$S = \int\limits_1^4 {\left| {\sqrt x - x + 2} \right|dx} $$ = \int\limits_1^4 {\left( {\sqrt x - x + 2} \right)dx} $$ = \left. {\left( {\frac{2}{3}{x^{\frac{3}{2}}} - \frac{{{x^2}}}{2} + 2x} \right)} \right|_1^4$$ = \frac{{16}}{3} - \frac{{13}}{6} = \frac{{19}}{6}$.

Câu 5/15

Ta biết rằng hàm cầu liên quan đến giá p của một sản phẩm với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm với mức độ sẵn sàng cung cấp sản phẩm của nhà sản xuất. Điểm cắt nhau (x₀; p₀) của đồ thị hàm cầu p = D(x) và đồ thị hàm cung p = S(x) được gọi là điểm cân bằng.

Các nhà kinh tế gọi diện tích của hình giới hạn bởi đồ thị hàm cầu, đường ngang p = p₀ và đường thẳng đứng x = 0 là thặng dư tiêu dùng. Tương tự, diện tích của hình giới hạn bởi đồ thị của hàm cung, đường nằm ngang p = p₀ và đường thẳng đứng x = 0 được gọi là thặng dư sản xuất, như trong Hình 4.19.

(Theo R.Larson, Brief Calculus: An Applied Approach, 8^th edition, Cengage Learning, 2009).

Giả sử hàm cung và hàm cầu của một loại sản phẩm được mô hình hóa bởi:

Hàm cầu: p = −0,36x + 9 và hàm cung: p = 0,14x + 2, trong đó x là số đơn vị sản phẩm. Tìm thặng dư tiêu dùng và thặng dư sản xuất cho sản phẩm này.

Xem đáp án

Lời giải

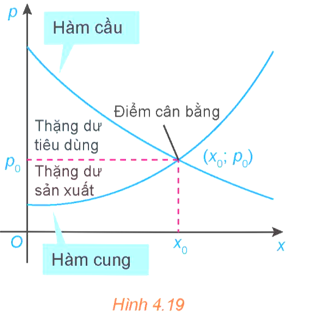
Hoành độ điểm cân bằng là nghiệm của phương trình:

−0,36x + 9 = 0,14x + 2 Û x = 14.

Tọa độ điểm cân bằng là (14; 3,96).

Thặng dư tiêu dùng là:

${S_1} = \int\limits_0^{14} {\left| { - 0,36x + 9 - 3,96} \right|} dx$$ = \int\limits_0^{14} {\left| { - 0,36x + 5,04} \right|} dx$$ = \int\limits_0^{14} {\left( { - 0,36x + 5,04} \right)} dx$

$ = \left. {\left( { - 0,18{x^2} + 5,04x} \right)} \right|_0^{14} = 35,28$.

Thặng dư sản xuất là:

${S_2} = \int\limits_0^{14} {\left| {3,96 - 0,14x - 2} \right|} dx$$ = \int\limits_0^{14} {\left| {1,96 - 0,14x} \right|} dx$$ = \int\limits_0^{14} {\left( {1,96 - 0,14x} \right)} dx$

$ = \left. {\left( {1,96x - 0,07{x^2}} \right)} \right|_0^{14}$$ = 13,72$.

Câu 6/15

Xét hình trụ có bán kính đáy R, có trục là trục hoành Ox, nằm giữa hai mặt phẳng x = a và x = b (a < b) (H.4.20).

a) Tính thể tích V của hình trụ.

b) Tính diện tích mặt cắt S(x) khi cắt hình trụ bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x (a ≤ x ≤ b). Từ đó tính $\int_{a}^{b} S (x) d x$ và so sánh với V.

Xem đáp án

Lời giải

a) Độ dài chiều cao hình trụ là: h = b – a.

Thể tích của hình trụ là: V = πR²h = πR²(b – a).

b) Diện tích mặt cắt S(x) khi cắt hình trụ bởi mặt phẳng vuông góc với trục Ox là

S(x) = πR².

Ta có $\int\limits_a^b {S\left( x \right)} dx$\[ = \int\limits_a^b {\pi {R^2}} dx\]\[ = \left. {\left( {\pi {R^2}x} \right)} \right|_a^b\]\[ = \pi {R^2}\left( {b - a} \right)\].

Vậy $V = \int\limits_a^b {S\left( x \right)} dx$.

Câu 7/15