Giải SBT Toán 12 Tập 2 KNTT Bài 17. Phương trình mặt cầu có đáp án
39 người thi tuần này 4.6 356 lượt thi 7 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Lời giải
a) Gọi I(x; y; z) là trung điểm của AB, ta có:
\(\left\{ \begin{array}{l}x = \frac{{2 + 2}}{2} = 2\\y = \frac{{1 + 1}}{2} = 1\\z = \frac{{1 + 3}}{2} = 2\end{array} \right.\)⇒ I(2; 1; 2).
Mặt cầu đường kính AB có tâm là I(2; 1; 2) và bán kính R = IA.
IA = \(\sqrt {{{\left( {2 - 2} \right)}^2} + {{\left( {1 - 1} \right)}^2} + {{\left( {2 - 1} \right)}^2}} \) = 1.
Vậy phương trình mặt cầu đường kính AB là:
(x – 2)2 + (y – 1)2 + (z – 2)2 = 12.
⇔ (x – 2)2 + (y – 1)2 + (z – 2)2 = 1.
b) Mặt cầu (S) tâm O và đi qua A có bán kính R = OA.
OA = \(\sqrt {{{\left( {2 - 0} \right)}^2} + {{\left( {1 - 0} \right)}^2} + {{\left( {1 - 0} \right)}^2}} \)= \(\sqrt 6 \).
Vậy phương trình mặt cầu (S) là: (x – 0)2 + (y – 0)2 + (z – 0)2 = \({\left( {\sqrt 6 } \right)^2}\).
⇔ x2 + y2 + z2 = 6.
Lời giải
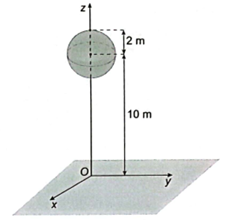
Do mặt cầu (S) tiếp xúc với mặt phẳng (P) nên R = d(I, (P)).
Ta có: R = d(I, (P)) = \(\frac{{\left| {2 + 2.( - 1) + 2.2 - 10} \right|}}{{\sqrt {{1^2} + {2^2} + {2^2}} }}\) = 2.
Vậy phương trình mặt cầu (S) là: (x – 2)2 + (y + 1)2 + (z – 2)2 = 22.
⇔ (x – 2)2 + (y + 1)2 + (z – 2)2 = 4.
Lời giải
a) Ta có (S): (x – 1)2 + y2 + (z + 2)2 = 9
⇔ (x – 1)2 + (y – 0)2 + (z – (−2))2 = 32.
Vậy mặt cầu (S) có tâm I(1; 0; −2) và bán kính R = 3.
b) Ta có: IA = \(\sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( {2 - 0} \right)}^2} + {{\left( { - 1 + 2} \right)}^2}} \) = \(\sqrt 6 \) < 3.
Do đó, điểm A nằm trong mặt cầu (S).
Lời giải
a) Phương trình có các hệ số a = −1, b = 0, c = 2 và d = 2.
⇒ a2 + b2 + c2 – d = (−1)2 + 02 + 22 – 2 = 3 > 0.
Do đó, phương trình đã cho là phương trình mặt cầu, hơn nữa mặt cầu có tâm là
I(−1; 0; 2) và bán kính R = \(\sqrt 3 \).
b) Phương trình có các hệ số a = 1, b = −1, c = −1 và d = 7.
⇒ a2 + b2 + c2 – d = 12 + (−1)2 + (−1)2 – 7 = −4 < 0.
Do đó, phương trình đã cho không phải là phương trình mặt cầu.
c) Ta có: 3x2 + 3y2 + 3z2 + 12x – 6y + 6z + 2 = 0.
⇔ x2 + y2 + z2 + 4x – 2y + 2z + \(\frac{2}{3}\) = 0.
Phương trình có các hệ số: a = −2, b =1, c = −1 và d = \(\frac{2}{3}\).
⇒ a2 + b2 + c2 – d = (−2)2 + 12 + (−1)2 − \(\frac{2}{3}\) = \(\frac{{16}}{3}\) > 0.
Do đó, phương trình đã cho là phương trình mặt cầu có tâm I(−2; 1; −1) và R = \(\frac{{4\sqrt 3 }}{3}\).
Lời giải
Theo đề bài, tâm I thuộc trục Ox nên I(x; 0; 0).
(S) đi qua hai điểm A và B nên IA = IB.
⇒ (x – 1)2 + (0 – 2)2 + (0 – 1)2 = (x + 1)2 + (0 + 2)2 + (0 – 3)2
⇒ x2 – 2x + 6 = x2 + 2x + 14
⇔ x = −2.
Do đó, tâm I(−2; 0; 0) và bán kính IA = \(\sqrt {14} \).
Phương trình mặt cầu cần tìm là: (x + 2)2 + y2 + z2 = 14.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.