Giải SGK Toán 12 KNTT Bài 12. Tích phân có đáp án
53 người thi tuần này 4.6 787 lượt thi 17 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Lời giải
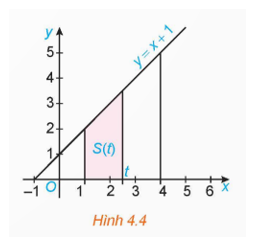
Sau khi học xong bài này, ta giải quyết bài toán này như sau:
Ô tô dừng lại khi v(t) = 0. Tức là −40t + 20 = 0 Û t = 0,5 giây.
Từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển được quãng đường là:
(m).
Vậy quãng đường ô tô di chuyển được là 5 mét.
Lời giải
a)
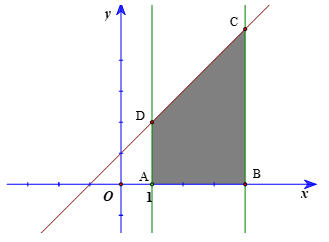
Kí hiệu A(1; 0), B(4; 0) và C, D lần lượt là giao điểm của đường thẳng x = 4; x = 1 với đường thẳng y = x + 1.
Khi đó C(4; 5), D(1; 2).
Ta có: AD = 2; BC = 5; AB = 3.
Khi đó diện tích hình thang T là \(S = \frac{{\left( {AD + BC} \right).AB}}{2} = \frac{{\left( {2 + 5} \right).3}}{2} = \frac{{21}}{2}\).
b)
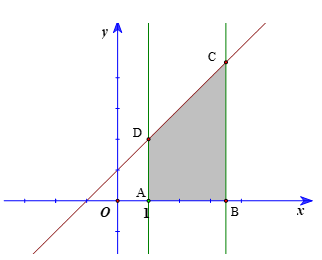
Gọi A(1; 0), B(t; 0), t ∈ [1; 4] và C, D lần lượt là giao điểm của đường thẳng x = t; x = 1 với đường thẳng y = x + 1.
Khi đó C(t; t + 1); D(1; 2).
Do đó AB = t – 1; AD = 2; BC = t + 1.
Khi đó diện tích hình thang ABCD là
\(S\left( t \right) = \frac{{\left( {AD + BC} \right).AB}}{2} = \frac{{\left( {t + 3} \right).\left( {t - 1} \right)}}{2} = \frac{{{t^2} + 2t - 3}}{2}.\)
c) Có \(S\left( t \right) = \frac{{{t^2} + 2t - 3}}{2}\)\( \Rightarrow S'\left( t \right) = {\left( {\frac{{{t^2} + 2t - 3}}{2}} \right)^\prime } = \frac{{2\left( {t + 1} \right)}}{2} = t + 1 = f\left( t \right)\).
Do đó S(t) là một nguyên hàm của hàm số f(t) = t + 1, t ∈ [1; 4].
Có \(S\left( 4 \right) = \frac{{{4^2} + 2.4 - 3}}{2} = \frac{{21}}{2};S\left( 1 \right) = \frac{{{1^2} + 2.1 - 3}}{2} = 0\).
Do đó S(4) – S(1) = S.
Lời giải
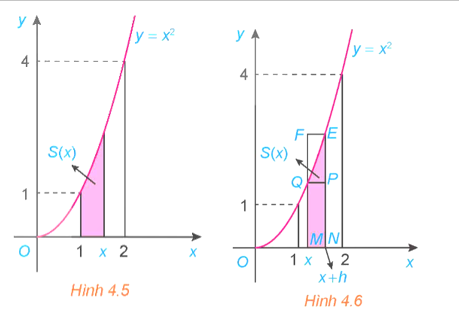
a) Với h > 0, x + h < 2, kí hiệu SMNPQ và SMNEF lần lượt là diện tích các hình chữ nhật MNPQ và MNEF, ta có: SMNPQ ≤ S(x + h) – S(x) ≤ SMNEF
hay hx2 ≤ S(x + h) – S(x) ≤ h(x + h)2.
Suy ra \(0 \le \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2} \le 2xh + {h^2}\).
b) Với h < 0 và x + h > 1, kí hiệu SMNPQ và SMNEF lần lượt là diện tích các hình chữ nhật MNPQ và MNEF, ta có SMNPQ ≤ S(x + h) – S(x) ≤ SMNEF
hay h(x+h)2 ≤ S(x + h) – S(x) ≤ hx2.
Suy ra \(2xh + {h^2} \le \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2} \le 0\).
c) Dựa vào kết quả của câu a, b ta suy ra với mọi h ≠ 0, ta có:
\(\left| {\frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2}} \right| \le 2x\left| h \right| + {h^2}\).
Suy ra \(S'\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} = {x^2},\forall x \in \left( {1;2} \right)\).
d) Vì S(1) = 0 nên \(S\left( 1 \right) = \frac{{{1^3}}}{3} + C = 0 \Rightarrow C = - \frac{1}{3}\).
Vậy \(S\left( x \right) = \frac{{{x^3}}}{3} - \frac{1}{3}\).
Ta có \(S = S\left( 2 \right) = \frac{{{2^3}}}{3} - \frac{1}{3} = \frac{7}{3}\).
Giả sử \(F\left( x \right) = \frac{{{x^3}}}{3}\) là một nguyên hàm của f(x) = x2 trên [1; 2].
Khi đó \(F\left( 1 \right) = \frac{1}{3};F\left( 2 \right) = \frac{8}{3}\). Ta thấy \(F\left( 2 \right) - F\left( 1 \right) = \frac{7}{3} = S\).
Lời giải
Vì F(x) và G(x) là hai nguyên hàm của f(x) trên đoạn [a; b] nên tồn tại một hằng số C sao cho F(x) = G(x) + C.
Do đó F(b) – F(a) = G(b) + C – G(a) – C = G(b) – G(a).
Lời giải
a) \(\int\limits_0^1 {{e^x}dx} = \left. {{e^x}} \right|_0^1 = e - 1\).
b) \(\int\limits_1^e {\frac{1}{x}} dx = \left. {\ln \left| x \right|} \right|_1^e = \ln e - \ln 1 = 1\).
c) \(\int\limits_0^{\frac{\pi }{2}} {\sin xdx} = \left. { - \cos x} \right|_0^{\frac{\pi }{2}} = - \cos \frac{\pi }{2} + \cos 0 = 1.\)
d) \(\int\limits_{\frac{\pi }{6}}^{\frac{\pi }{3}} {\frac{{dx}}{{{{\sin }^2}x}}} = \left. { - \cot x} \right|_{\frac{\pi }{6}}^{\frac{\pi }{3}} = - \cot \frac{\pi }{3} + \cot \frac{\pi }{6} = - \frac{{\sqrt 3 }}{3} + \sqrt 3 = \frac{{2\sqrt 3 }}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.