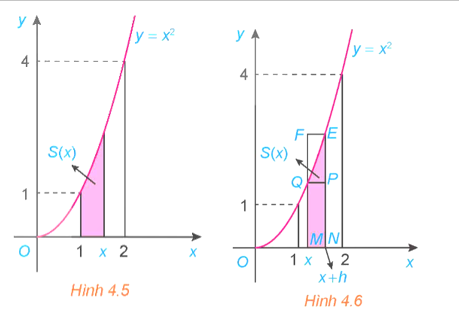
Xét hình thang cong giới hạn bởi đồ thị y = x², trục hoành và hai đường thẳng x = 1, x = 2. Ta muốn tính diện tích S của hình thang cong này.

a) Với mỗi x ∈ [1; 2], gọi S(x) là diện tích phần hình thang cong đã cho nằm giữa hai đường thẳng vuông góc với trục Ox tại điểm có hoành độ bằng 1 và x (H.4.5).

Cho h > 0 sao cho x + h < 2. So sánh hiệu S(x + h) – S(x) với diện tích hai hình chữ nhật MNPQ và MNEF (H.4.6). Từ đó suy ra $0 \le \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2} \le 2xh + {h^2}$.

b) Cho h < 0 sao cho x + h > 1. Tương tự phần a, đánh giá hiệu S(x) – S(x + h) và từ đó suy ra $2xh + {h^2} \le \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2} \le 0$.

c) Từ kết quả phần a và phần b, suy ra với mọi h ≠ 0, ta có $\left| {\frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2}} \right| \le 2x\left| h \right| + {h^2}$.

Từ đó chứng minh S'(x) = x², x ∈ (1; 2).

Người ta chứng minh được S'(1) = 1, S'(2) = 4, tức là S(x) là một nguyên hàm của x² trên [1; 2].

d) Từ kết quả của phần c, ta có $S\left( x \right) = \frac{{{x^3}}}{3} + C$. Sử dụng điều này với lưu ý S(1) = 0 và diện tích cần tính S = S(2), hãy tính S.

Gọi F(x) là một nguyên hàm tùy ý của f(x) = x² trên [1; 2]. Hãy so sánh S và F(2) – F(1).

Xem lời giải

Câu hỏi trong đề: Giải SGK Toán 12 KNTT Bài 12. Tích phân có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) Với h > 0, x + h < 2, kí hiệu S_MNPQ và S_MNEF lần lượt là diện tích các hình chữ nhật MNPQ và MNEF, ta có: S_MNPQ ≤ S(x + h) – S(x) ≤ S_MNEF

hay hx² ≤ S(x + h) – S(x) ≤ h(x + h)².

Suy ra $0 \le \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2} \le 2xh + {h^2}$.

b) Với h < 0 và x + h > 1, kí hiệu S_MNPQ và S_MNEF lần lượt là diện tích các hình chữ nhật MNPQ và MNEF, ta có S_MNPQ ≤ S(x + h) – S(x) ≤ S_MNEF

hay h(x+h)² ≤ S(x + h) – S(x) ≤ hx².

Suy ra $2xh + {h^2} \le \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2} \le 0$.

c) Dựa vào kết quả của câu a, b ta suy ra với mọi h ≠ 0, ta có:

$\left| {\frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2}} \right| \le 2x\left| h \right| + {h^2}$.

Suy ra $S'\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} = {x^2},\forall x \in \left( {1;2} \right)$.

d) Vì S(1) = 0 nên $S\left( 1 \right) = \frac{{{1^3}}}{3} + C = 0 \Rightarrow C = - \frac{1}{3}$.

Vậy $S\left( x \right) = \frac{{{x^3}}}{3} - \frac{1}{3}$.

Ta có $S = S\left( 2 \right) = \frac{{{2^3}}}{3} - \frac{1}{3} = \frac{7}{3}$.

Giả sử $F\left( x \right) = \frac{{{x^3}}}{3}$ là một nguyên hàm của f(x) = x² trên [1; 2].

Khi đó $F\left( 1 \right) = \frac{1}{3};F\left( 2 \right) = \frac{8}{3}$. Ta thấy $F\left( 2 \right) - F\left( 1 \right) = \frac{7}{3} = S$.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Giả sử lợi nhuận biên (tính bằng triệu đồng) của một sản phẩm được mô hình hóa bằng công thức P'(x) = −0,0005x + 12,2. Ở đây P(x) là lợi nhuận (tính bằng triệu đồng) khi bán được x đơn vị sản phẩm.

a) Tìm sự thay đổi của lợi nhuận khi doanh số tăng từ 100 lên 101 sản phẩm.

b) Tìm sự thay đổi của lợi nhuận khi doanh số tăng từ 100 lên 110 sản phẩm.

Xem đáp án

Lời giải

a) Sự thay đổi của lợi nhuận khi doanh số tăng từ 100 lên 101 sản phẩm là:

$\int\limits_{100}^{101} {P'\left( x \right)} dx = \int\limits_{100}^{101} {\left( { - 0,0005x + 12,2} \right)} dx$$ = \left. {\left( { - \frac{1}{{4000}}{x^2} + 12,2x} \right)} \right|_{100}^{101}$

= 1229,64975 – 1217,5 = 12,14975 triệu đồng.

b) Sự thay đổi của lợi nhuận khi doanh số tăng từ 100 lên 110 sản phẩm là

$\int\limits_{100}^{110} {P'\left( x \right)} dx = \int\limits_{100}^{110} {\left( { - 0,0005x + 12,2} \right)} dx$$ = \left. {\left( { - \frac{1}{{4000}}{x^2} + 12,2x} \right)} \right|_{100}^{110}$

= 1338,975 – 1217,5 = 121,475 triệu đồng.

Câu 2

Một vật chuyển động dọc theo một đường thẳng sao cho vận tốc của nó tại thời điểm t (giây) là v(t) = t² – t – 6 (m/s).

a) Tìm độ dịch chuyển của vật trong khoảng thời gian 1 ≤ t ≤ 4, tức là tính $\int_{1}^{4} v (t) d t$ .

b) Tìm tổng quãng đường vật đi được trong khoảng thời gian này, tức là tính $\int_{1}^{4} |v (t)| d t .$

Xem đáp án

Lời giải

a) Độ dịch chuyển của vật trong khoảng thời gian 1 ≤ t ≤ 4 là

$\int\limits_1^4 {v\left( t \right)} dt = \int\limits_1^4 {\left( {{t^2} - t - 6} \right)} dt$$ = \int\limits_1^4 {{t^2}} dt - \int\limits_1^4 t dt - 6\int\limits_1^4 {dt} $$ = \left. {\left( {\frac{{{t^3}}}{3} - \frac{{{t^2}}}{2} - 6t} \right)} \right|_1^4$$ = - \frac{{32}}{3} + \frac{{37}}{6} = - \frac{9}{2}$.

b) Tổng quãng đường vật đi được trong khoảng thời gian này là

$\int\limits_1^4 {\left| {v\left( t \right)} \right|} dt$$ = \int\limits_1^4 {\left| {{t^2} - t - 6} \right|} dt$$ = \int\limits_1^3 {\left| {{t^2} - t - 6} \right|} dt + \int\limits_3^4 {\left| {{t^2} - t - 6} \right|} dt$

$ = - \int\limits_1^3 {\left( {{t^2} - t - 6} \right)} dt + \int\limits_3^4 {\left( {{t^2} - t - 6} \right)} dt$$ = - \left. {\left( {\frac{{{t^3}}}{3} - \frac{{{t^2}}}{2} - 6t} \right)} \right|_1^3 + \left. {\left( {\frac{{{t^3}}}{3} - \frac{{{t^2}}}{2} - 6t} \right)} \right|_3^4$$ = \frac{{27}}{2} - \frac{{37}}{6} - \frac{{32}}{3} + \frac{{27}}{2} = \frac{{61}}{6}$.

Câu 3