Giải SBT Toán 12 Tập 2 KNTT Bài 13. Ứng dụng hình học của tích phân có đáp án

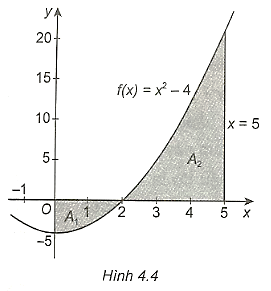
a) Diện tích cần tính là:

S = \(\int\limits_0^5 {\left| {{x^2} - 4} \right|dx}  = \int\limits_0^2 {\left| {{x^2} - 4} \right|dx}  + \int\limits_2^5 {\left| {{x^2} - 4} \right|dx} \)

                         = \(\int\limits_0^2 {\left( {4 - {x^2}} \right)dx}  + \int\limits_2^5 {\left( {{x^2} - 4} \right)dx} \)

                         = \(\left. {\left( {4x - \frac{{{x^3}}}{3}} \right)} \right|_0^2 + \left. {\left( {\frac{{{x^3}}}{3} - 4x} \right)} \right|_2^5\)

                         = 4.2 – \(\frac{8}{3}\) − 4.0 + \(\frac{0}{3}\) + \(\frac{{{5^3}}}{3}\) − 4.5 – \(\frac{8}{3}\) + 4.2 = \(\frac{{97}}{3}\).

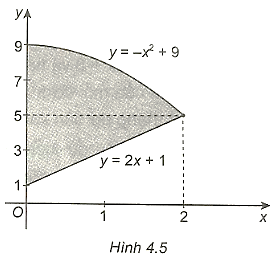
b) Diện tích cần tính là:

S = \(\int\limits_0^2 {\left| { - {x^2} + 9 - \left( {2x + 1} \right)} \right|dx} \) = \(\int\limits_0^2 {\left| { - {x^2} - 2x + 8} \right|} dx\)

                                         = \(\int\limits_0^2 {\left( { - {x^2} - 2x + 8} \right)dx} \)

                                         = \(\left. {\left( {\frac{{ - {x^3}}}{3} - {x^2} + 8x} \right)} \right|_0^2\) = \(\frac{{28}}{3}\).

a) Ta có: (x – 1)3 ≥ x – 1, với mọi x ∈ [0; 1].

Do đó, diện tích cần tính là:

S = \(\int\limits_0^1 {\left| {{{\left( {x - 1} \right)}^3} - \left( {x - 1} \right)} \right|dx} \) = \(\int\limits_0^1 {\left[ {{{\left( {x - 1} \right)}^3} - \left( {x - 1} \right)} \right]dx} \)

                                         = \(\int\limits_0^1 {\left( {{x^3} - 3{x^2} + 2x} \right)} dx\)

                                         = \(\left. {\left( {\frac{{{x^4}}}{4} - {x^3} + {x^2}} \right)} \right|_0^1\) = \(\frac{1}{4}\).

b) Ta có: x3 + 2x2 – 3x – x2 – 3x = x3 + x2 – 6x = x(x – 2)(x + 3) ≥ 0, với mọi x ∈ [−3; 0].

Do đó, diện tích cần tính là:

S = \(\int\limits_{ - 3}^0 {\left| {{x^3} + 2{x^2}--3x--{x^2}--3x} \right|} dx\)

   = \(\int\limits_{ - 3}^0 {\left| {{x^3} + {x^2} - 6x} \right|dx} \)

   = \(\int\limits_{ - 3}^0 {\left( {{x^3} + {x^2} - 6x} \right)dx} \)

   = \(\left. {\left( {\frac{{{x^4}}}{4} + \frac{{{x^3}}}{3} - 3{x^2}} \right)} \right|_{ - 3}^0\)

   = \(\frac{{63}}{4}\).

a) Ta có: ex ≥ 1 ≥ \(\sqrt x \), với mọi x ∈ [0; 1], nên diện tích cần tính là:

S = \(\int\limits_0^1 {\left| {{e^x} - \sqrt x } \right|dx}  = \int\limits_0^1 {\left( {{e^x} - \sqrt x } \right)dx} \) = \(\left. {\left( {{e^x} - \frac{2}{3}{x^{\frac{3}{2}}}} \right)} \right|_0^1\) = e − \(\frac{5}{3}\).

b) Vì cosx ≥ \(\frac{1}{2}\), với mọi x ∈ \(\left[ {0;\frac{\pi }{3}} \right]\), nên diện tích cần tính là:

S = \(\int\limits_0^{\frac{\pi }{3}} {\left| {\cos x - \frac{1}{2}} \right|dx}  = \int\limits_0^{\frac{\pi }{3}} {\left( {\cos x - \frac{1}{2}} \right)dx}  = \left. {\left( {\sin x - \frac{1}{2}} \right)} \right|_0^{\frac{\pi }{3}} = \frac{{\sqrt 3 }}{2} - \frac{\pi }{6}\).

a) Thể tích cần tính là:

V = π\(\int\limits_1^4 {{{\left( {2\sqrt x } \right)}^2}} dx = \pi \int\limits_1^4 {4xdx = \left. {\pi 2{x^2}} \right|_1^4 = 30\pi } \).

b)

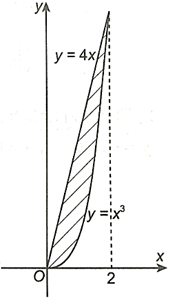
Đồ thị hàm số y = 4x nằm phía trên đồ thị hàm số y = x3 so với trục hoành, với mọi

x ∈ [0; 2].

Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường thẳng y = 4x, y = 0, x = 0, x = 2 quanh trục Ox là:

V1 = \(\pi \int\limits_0^2 {{{\left( {4x} \right)}^2}dx}  = \pi \int\limits_0^2 {16{x^2}dx}  = \frac{{128\pi }}{3}\).

Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường y = x3, y = 0, x = 0, x = 2 quanh trục Ox là:

V2 = \(\pi \int\limits_0^2 {{{\left( {{x^3}} \right)}^2}dx}  = \pi \int\limits_0^2 {{x^6}dx}  = \frac{{128\pi }}{7}\).

Thể tích cần tính là: V = V1 – V2 = \(\frac{{128\pi }}{3}\) − \(\frac{{128\pi }}{7}\) = \(\frac{{512\pi }}{{21}}\).

a) Ta có đồ thị hàm số như sau:

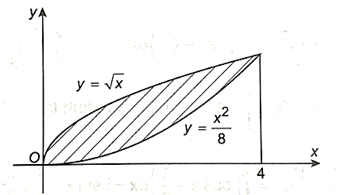
Quan sát đồ thị, ta thấy đồ thị hàm số y = \(\sqrt x \) nằm phía trên đồ thị hàm số y = \(\frac{{{x^2}}}{8}\) so với trục hoành, với x ∈ [0; 4].

Diện tích cần tính là:

S = \(\int\limits_0^4 {\left| {\sqrt x  - \frac{{{x^2}}}{8}} \right|} dx = \int\limits_0^4 {\left( {\sqrt x  - \frac{{{x^2}}}{8}} \right)} dx = \left. {\left( {\frac{2}{3}x\sqrt x  - \frac{{{x^3}}}{{24}}} \right)} \right|_0^4 = \frac{8}{3}\).

b) Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường y = \(\sqrt x \),

y = 0, x = 0, x = 4 quanh trục Ox là:

V1 = \(\pi \int\limits_0^4 {{{\left( {\sqrt x } \right)}^2}} dx = \pi \int\limits_0^4 {xdx = \left. {\frac{{\pi {x^2}}}{2}} \right|_0^4 = 8\pi .} \)

Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường y = \(\frac{{{x^2}}}{8}\),

y = 0, x = 0, x = 2 quanh trục Ox là:

V2 = \(\pi \int\limits_0^4 {{{\left( {\frac{{{x^2}}}{8}} \right)}^2}} dx = \pi \int\limits_0^4 {\frac{{{x^4}}}{{64}}dx = \left. {\frac{{\pi {x^5}}}{{320}}} \right|_0^4 = \frac{{16\pi }}{5}.} \)

Thể tích cần tính là:

V = V1 – V2 = \(8\pi  - \frac{{16\pi }}{5} = \frac{{24\pi }}{5}\).