Câu hỏi:
22/08/2024 1,833
Hàm cầu và hàm cung của một sản phẩm được mô hình hóa bởi:
Hàm cầu: p = −0,2x + 8 và hàm cung: p = 0,1x + 2, trong đó x là số đơn vị sản phẩm, p là giá của mỗi đơn vị sản phẩm (tính bằng triệu đồng). Tìm thặng dư tiêu dùng và thặng dư sản xuất đối với sản phẩm này.
Hàm cầu và hàm cung của một sản phẩm được mô hình hóa bởi:
Hàm cầu: p = −0,2x + 8 và hàm cung: p = 0,1x + 2, trong đó x là số đơn vị sản phẩm, p là giá của mỗi đơn vị sản phẩm (tính bằng triệu đồng). Tìm thặng dư tiêu dùng và thặng dư sản xuất đối với sản phẩm này.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét phương trình −0,2x + 8 = 0,1x + 2 ⇔ x = 20, khi đó p = −0,2.20 + 8 = 4.
Thặng dư tiêu dùng là:
\(\int\limits_0^{20} {\left( { - 0,2x + 8 - 3} \right)} dx = \left. {\left( { - 0,1 + 4x} \right)} \right|_0^{20}\) = 40 (triệu đồng).
Thặng dư sản xuất là:
\(\int\limits_0^{20} {\left[ {4 - \left( {0,1x + 2} \right)} \right]dx = } \left. {\left( {2x - 0,1.\frac{{{x^2}}}{2}} \right)} \right|_0^{20}\) = 20 (triệu đồng).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
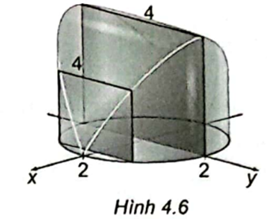
Ta có hình sau:
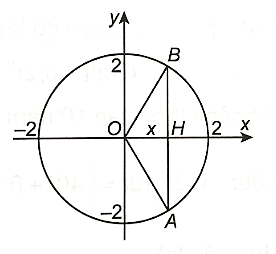
Mỗi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ bằng x (−2 ≤ x ≤ 2) cắt vật thể theo mặt cắt là hình vuông có độ dài cạnh là AB = 2BH = \(2\sqrt {4 - {x^2}} \).
Khi đó diện tích mặt cắt là 4(4 – x2).
Vậy thể tích của vật thể là: V = \(\int\limits_{ - 2}^2 {4\left( {4 - {x^2}} \right)} dx = \frac{{128}}{3}\).
Lời giải
a) Diện tích cần tính là:
S = \(\int\limits_0^5 {\left| {{x^2} - 4} \right|dx} = \int\limits_0^2 {\left| {{x^2} - 4} \right|dx} + \int\limits_2^5 {\left| {{x^2} - 4} \right|dx} \)
= \(\int\limits_0^2 {\left( {4 - {x^2}} \right)dx} + \int\limits_2^5 {\left( {{x^2} - 4} \right)dx} \)
= \(\left. {\left( {4x - \frac{{{x^3}}}{3}} \right)} \right|_0^2 + \left. {\left( {\frac{{{x^3}}}{3} - 4x} \right)} \right|_2^5\)
= 4.2 – \(\frac{8}{3}\) − 4.0 + \(\frac{0}{3}\) + \(\frac{{{5^3}}}{3}\) − 4.5 – \(\frac{8}{3}\) + 4.2 = \(\frac{{97}}{3}\).
b) Diện tích cần tính là:
S = \(\int\limits_0^2 {\left| { - {x^2} + 9 - \left( {2x + 1} \right)} \right|dx} \) = \(\int\limits_0^2 {\left| { - {x^2} - 2x + 8} \right|} dx\)
= \(\int\limits_0^2 {\left( { - {x^2} - 2x + 8} \right)dx} \)
= \(\left. {\left( {\frac{{ - {x^3}}}{3} - {x^2} + 8x} \right)} \right|_0^2\) = \(\frac{{28}}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận