Giải SBT Toán 12 Tập 2 KNTT Bài 12. Tích phân có đáp án

a) Ta có tích phân cần tính chính là diện tích của hình thang OABC, có đáy lớn AB = 7, đáy nhỏ CO = 1, đường cao OA = 3.

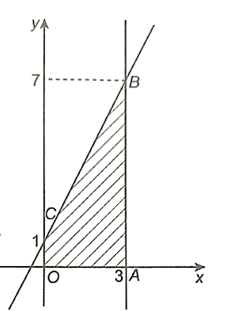
Do đó, \(\int\limits_0^3 {\left( {2x + 1} \right)dx} \) = S_OABC = \(\frac{1}{2}\left( {AB + CO} \right)OA = \frac{1}{2}\).(7 + 1).3 = 12.

b) Tích phân cần tích chính là diện tích của \(\frac{1}{4}\) hình tròn có tâm tại gốc tọa độ O và bán kính R = 4 (phần nằm ở góc phần tư thứ nhất của mặt phẳng tọa độ) như hình dưới đây.

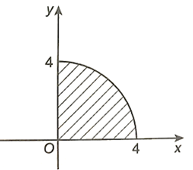
Do đó, \(\int\limits_0^4 {\sqrt {16 - {x^2}} dx} \)= \(\frac{1}{4}.\pi {.4^2}\) = 4π.

a) \(\int\limits_0^5 {\left[ {2f\left( x \right) + 3g\left( x \right)} \right]} dx\) = \(2\int\limits_0^5 {f\left( x \right)dx} + 3\int\limits_0^5 {g\left( x \right)dx} \)

                                       = 2.6 + 3.2 = 18.

b) \(\int\limits_0^5 {\left[ {2f\left( x \right) - 3g\left( x \right)} \right]} dx\) = \(2\int\limits_0^5 {f\left( x \right)dx} - 3\int\limits_0^5 {g\left( x \right)dx} \)

                                        = 2.6 – 3.2 = 6.

a) \(\int\limits_0^1 {{{\left( {1 - 2x} \right)}^2}} dx\) = \(\int\limits_0^1 {\left( {1 - 4x + 4{x^2}} \right)} dx\)

                          = \(\left. {\left( {x - 2{x^2} + \frac{4}{3}{x^3}} \right)} \right|_0^1\)

                          = \(\frac{1}{3}\).

b) \(\int\limits_1^4 {\frac{{x - 2}}{{\sqrt x }}dx} \) = \(\int\limits_1^4 {\left( {\sqrt x  - \frac{2}{{\sqrt x }}} \right)dx} \)

                      = \(\int\limits_1^4 {\left( {\sqrt x  - 2.{x^{\frac{{ - 1}}{2}}}} \right)dx} \)

                      = \(\left. {\left( {\frac{2}{3}x\sqrt x  - 4\sqrt x } \right)} \right|_1^4\)

                      = \(\frac{2}{3}\).

a) \(\int\limits_0^2 {\left| {2x - 1} \right|dx} \) = \(\int\limits_0^{\frac{1}{2}} {\left| {2x - 1} \right|dx} + \int\limits_{\frac{1}{2}}^2 {\left| {2x - 1} \right|dx} \)

                       = \(\int\limits_0^{\frac{1}{2}} {\left( {1 - 2x} \right)dx} + \int\limits_{\frac{1}{2}}^2 {\left( {2x - 1} \right)dx} \)

                       = \(\left. {\left( {x - {x^2}} \right)} \right|_0^{\frac{1}{2}} + \left. {\left( {{x^2} - x} \right)} \right|_{\frac{1}{2}}^2\) = \(\frac{5}{2}\).

b) \(\int\limits_{ - 2}^3 {\left| {x - 1} \right|dx} \) = \(\int\limits_{ - 2}^1 {\left| {x - 1} \right|dx} + \int\limits_1^3 {\left| {x - 1} \right|dx} \)

                      = \(\int\limits_{ - 2}^1 {\left( {1 - x} \right)dx} + \int\limits_1^3 {\left( {x - 1} \right)dx} \)

                      = \(\left. {\left( {x - \frac{1}{2}{x^2}} \right)} \right|_{ - 2}^1 + \left. {\left( {\frac{1}{2}{x^2} - x} \right)} \right|_1^3\)

                      = 1² − \(\frac{1}{2}\).1² – (−2) + \(\frac{1}{2}\).(−2)² + \(\frac{1}{2}\).3² – 3 − \(\frac{1}{2}\).1² + 1.

                      = \(\frac{{13}}{2}\).

a) \(\int\limits_0^{\frac{\pi }{2}} {\left( {3\cos x + 2\sin x} \right)dx} \) = \(\int\limits_0^{\frac{\pi }{2}} {3\cos xdx}  + \int\limits_0^{\frac{\pi }{2}} {2\sin xdx} \)

                                        = \(\left. {3\sin x} \right|_0^{^{\frac{\pi }{2}}} - \left. {2\cos x} \right|_0^{^{\frac{\pi }{2}}}\)

                                        = \(3\sin \frac{\pi }{2} - 3\sin 0 - 2\cos \frac{\pi }{2} + 2\cos 0\)

                                        = 5.

b) \(\int\limits_{\frac{\pi }{6}}^{\frac{\pi }{4}} {\left( {\frac{1}{{{{\cos }^2}x}} - \frac{1}{{{{\sin }^2}x}}} \right)dx} \) = \(\int\limits_{\frac{\pi }{6}}^{\frac{\pi }{4}} {\frac{1}{{{{\cos }^2}x}}dx}  - \int\limits_{\frac{\pi }{6}}^{\frac{\pi }{4}} {\frac{1}{{{{\sin }^2}x}}dx} \)

                                       = \(\left. {\tan x} \right|_{_{\frac{\pi }{6}}}^{^{\frac{\pi }{4}}} - \left. {\cot x} \right|_{_{\frac{\pi }{6}}}^{^{\frac{\pi }{4}}}\)

                                       = \(\tan \frac{\pi }{4} - \tan \frac{\pi }{6} - \cot \frac{\pi }{4} + \cot \frac{\pi }{6}\)

                                       = 2 − \(\frac{{4\sqrt 3 }}{3}\).