Giải SBT Toán 12 Tập 1 KNTT Bài 6. Vectơ trong không gian có đáp án
49 người thi tuần này 4.6 658 lượt thi 15 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Lời giải
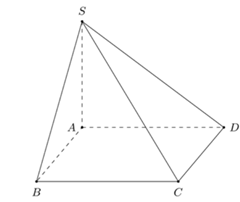
Cho hình chóp tứ giác S.ABCD. Trong các vectơ có điểm đầu và điểm cuối phân biệt thuộc tập {S, A, B, C, D}:
a) Những vectơ nào có điểm đầu là S?
b) Những vectơ nào có giá nằm trong mặt phẳng (SAB)?
c) Vectơ nào là vectơ đối của vectơ \(\overrightarrow {BC} \)?
Lời giải
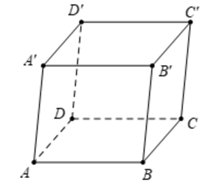
a) Ta có tứ giác ACC'A' là hình bình hành nên AC // A'C', suy ra \(\overrightarrow {A'C'} \) cùng phương với vectơ \(\overrightarrow {AC} \).
Do đó, các vec tơ \(\overrightarrow {CA} \), \(\overrightarrow {A'C'} \) và \(\overrightarrow {C'A'} \) cũng cùng phương với \(\overrightarrow {AC} \).
Vectơ cùng phương với vectơ \(\overrightarrow {AC} \) là: \(\overrightarrow {CA} \), \(\overrightarrow {A'C'} \) và \(\overrightarrow {C'A'} \).
b) Tứ giác ABC'D' là hình bình hành nên \(\overrightarrow {AD'} = \overrightarrow {BC'} \).
c) Vectơ đối của vectơ \(\overrightarrow {AA'} \) là: \(\overrightarrow {A'A} \), \(\overrightarrow {B'B} \), \(\overrightarrow {C'C} \), \(\overrightarrow {D'D} \).
Lời giải
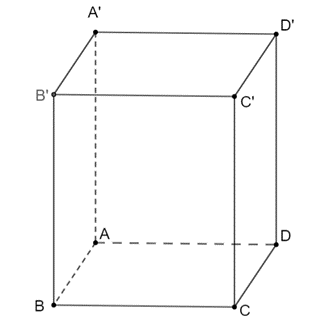
a) Ta có tam giác ABD vuông tại cân tại A và AB = AD = 1,
Suy ra \(\left| {\overrightarrow {BD} } \right|\) = BD = \(\sqrt {A{B^2} + A{D^2}} \)= \(\sqrt 2 \).
b) Tam giác CDD' vuông tại D có CD = AB = 1, DD' = AA' = 2.
Do đó, \(\left| {\overrightarrow {CD'} } \right|\) = CD' = \(\sqrt 5 \).
c) Do AB = AD = 1 nên đáy ABCD là hình vuông, suy ra AC = BD = \(\sqrt 2 \).
Tam giác ACC' vuông tại C, có AC = \(\sqrt 2 \) và CC' = 2.
Suy ra \(\left| {\overrightarrow {AC'} } \right|\) = AC' = \(\sqrt {C{{C'}^2} + A{C^2}} \) = \(\sqrt 6 \).
Lời giải
a) Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} = \)\(\overrightarrow {AC} \) + \(\overrightarrow {CD} \) = \(\overrightarrow {AD} \) = \(\overrightarrow {AE} + \overrightarrow {ED} \) = \(\overrightarrow {AE} - \overrightarrow {DE} \).
Vậy \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} = \overrightarrow {AE} - \overrightarrow {DE} \).
b) Ta có: \(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} = \overrightarrow {AE} + \overrightarrow {ED} \)
⇒ \(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AE} + \overrightarrow {ED} \)
⇔ \(\overrightarrow {AB} - \overrightarrow {ED} = \overrightarrow {AE} - \overrightarrow {BD} \)
⇔ \(\overrightarrow {AB} + \overrightarrow {DE} = \overrightarrow {AE} - \overrightarrow {BD} \)
Vậy ta có đpcm.
c) Ta có: \(\overrightarrow {BC} + \overrightarrow {CD} = \overrightarrow {BD} = \overrightarrow {BE} + \overrightarrow {ED} \)
⇒ \(\overrightarrow {BC} + \overrightarrow {CD} = \overrightarrow {BE} + \overrightarrow {ED} \)
⇔ \(\overrightarrow {BC} - \overrightarrow {ED} = \overrightarrow {BE} - \overrightarrow {CD} \)
⇔ \(\overrightarrow {BC} + \overrightarrow {DE} = \overrightarrow {BE} - \overrightarrow {CD} \)
Vậy ta có đpcm.
Lời giải
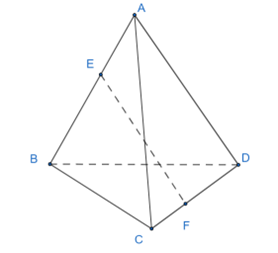
a) Ta có: \(\overrightarrow {EF} = \overrightarrow {EA} + \overrightarrow {AD} + \overrightarrow {DF} \)
= −\(\overrightarrow {AE} \) + \(\overrightarrow {AD} \) − \(\overrightarrow {FD} \)
= \(\overrightarrow {AD} \)− \(\frac{1}{3}\overrightarrow {AB} \) − \(\frac{2}{3}\overrightarrow {CD} \).
Vậy \(\overrightarrow {EF} = \overrightarrow {AD} - \frac{1}{3}\overrightarrow {AB} - \frac{2}{3}\overrightarrow {CD} \).
b) Ta có: \(\overrightarrow {EF} = \overrightarrow {EB} + \overrightarrow {BC} + \overrightarrow {CF} \)
= \(\frac{2}{3}\overrightarrow {AB} + \overrightarrow {CB} + \frac{1}{3}\overrightarrow {CD} \).
Vậy \(\overrightarrow {EF} = \overrightarrow {BC} + \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {CD} \).
c) Từ câu a và b, ta có:
\(3\overrightarrow {EF} = \left( {\overrightarrow {AD} - \frac{1}{3}\overrightarrow {AB} - \frac{2}{3}\overrightarrow {CD} } \right) + 2\left( {\frac{2}{3}\overrightarrow {AB} + \overrightarrow {CB} + \frac{1}{3}\overrightarrow {CD} } \right)\)
= \(\overrightarrow {AD} - \frac{1}{3}\overrightarrow {AB} - \frac{2}{3}\overrightarrow {CD} \) + \(\frac{4}{3}\overrightarrow {AB} + 2\overrightarrow {CB} + \frac{2}{3}\overrightarrow {CD} \)
= \(\overrightarrow {AD} \) + \(\left( { - \frac{1}{3}\overrightarrow {AB} + \frac{4}{3}\overrightarrow {AB} } \right)\) + \(\left( { - \frac{2}{3}\overrightarrow {CD} + \frac{2}{3}\overrightarrow {CD} } \right)\) + \(2\overrightarrow {CB} \)
= \(\overrightarrow {AD} \) + \(2\overrightarrow {CB} \) + \(\overrightarrow {AB} \)
⇒ \(\overrightarrow {EF} = \frac{1}{3}\overrightarrow {AD} + \frac{2}{3}\overrightarrow {BC} + \frac{1}{3}\overrightarrow {AB} \).
Vậy ta có đpcm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.