Giải SBT Toán 12 Tập 2 KNTT Bài tập ôn tập cuối năm có đáp án

35 người thi tuần này 4.6 525 lượt thi 45 câu hỏi

Câu 1/45

Giá trị của tham số m để hàm số y = \(\frac{1}{3}\)x³ – mx² + 4x – 2023 đạt cực trị tại x = −2 là

A. Không tồn tại m.

B. m = −2.

C. m = 2.

D. m = 0.

Lời giải

Đáp án đúng là: A

Tập xác định: D = ℝ.

Ta có: y' = x² – 2mx + 4.

Để hàm số đạt cực đại tại x = −2 thì y'(−2) = 0 hay (−2)² − 2m(−2) + 4 = 0 ⇔ m = 2.

Thử lại với m = 2, ta có y' = x² – 2x + 4 = (x – 2)² ≥ 0, ∀x ∈ ℝ.

Do đó, với m = 2 hàm số đồng biến trên ℝ, nên không có cực trị.

Vậy không tồn tại giá trị m thỏa mãn yêu cầu bài toán.

Câu 2/45

Cho hàm số y = x³ + 3x² + 1 có đồ thị (C). Xét đường thẳng đi qua điểm A(−3; 1) và có hệ số góc k. Điều kiện của k để đường thẳng đó cắt đồ thị (C) tại ba điểm phân biệt là

A. 0 < k < 1.

B. k > 0.

C. 1 < k < 9.

D. 0 < k ≠ 9.

Lời giải

Đáp án đúng là: D

Phương trình đường thẳng đi qua A(−3; 1) và có hệ số góc k là: y = k(x + 3) + 1.

Xét phương trình hoành độ giao điểm, ta có:

x³ + 3x² + 1 = k(x + 3) + 1

⇔ x³ + 3x² – k(x + 3) = 0

⇔ x²(x + 3) – k(x + 3) = 0

⇔ (x + 3)(x² – k) = 0

⇔ x = −3 hoặc x² = k.

Để đường thẳng cắt đồ thị (C) tại 3 điểm phân biệt thì x² = k có hai nghiệm phân biệt khác −3.

Do đó, k > 0 và k ≠ (−3)².

Vậy 0 < k ≠ 9.

Câu 3/45

Đồ thị trong hình vẽ dưới đây là của hàm số nào?

A. \(y = \frac{{{x^2} - 2x}}{{x + 1}}.\)

B. \(y = \frac{{{x^2} + 2x}}{{x + 1}}.\)

C. \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}.\)

D. \(y = \frac{{2x}}{{x + 1}}.\)

Lời giải

Đáp án đúng là: B

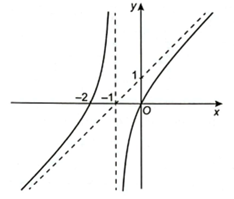
Cách 1:

Dựa vào đồ thị hàm số, ta thấy:

Đồ thị hàm số có tiệm cận đứng x = −1.

Tiệm cận xiên đi qua điểm (−1; 0) và (0; 1) có phương trình y = x + 1 nên loại A và D.

Dạng đồ thị hàm số cho thấy hàm đồng biến trên tập xác định.

Đồ thị hàm số đi qua điểm (−2; 0) nên loại C.

Chọn đáp án B.

Cách 2:

Xét các đáp án, nhận thấy đáp án B, ta có: \(y = \frac{{{x^2} + 2x}}{{x + 1}} = x + 1 - \frac{1}{{x + 1}}\) có đường tiệm cận đứng x = −1 và tiệm cận xiên y = x + 1.

Lại có y' = 1 + \(\frac{1}{{{{\left( {x + 1} \right)}^2}}}\) > 0, ∀x ≠ −1 nên hàm số đồng biến trên mỗi khoảng xác định (−∞; −1) và (−1; +∞).

Đồ thị hàm số đi qua điểm (−2; 0) nên đáp án thỏa mãn là B.

Câu 4/45

Tất cả các giá trị thực của tham số m để đường thẳng y = x + m – 1 cắt đồ thị hàm số y = \(\frac{{2x + 1}}{{x + 1}}\) tại hai điểm A, B thỏa mãn AB = \(2\sqrt 3 \) là

A. m = \(2 \pm \sqrt {10} .\)

B. m = \(4 \pm \sqrt 3 .\)

C. m = \(2 \pm \sqrt 3 .\)

D. m = \(4 \pm \sqrt {10} .\)

Lời giải

Đáp án đúng là: D

Xét phương trình hoành độ giao điểm, ta có:

x + m – 1 = \(\frac{{2x + 1}}{{x + 1}}\)

⇔ x² + (m – 2)x + m – 2 = 0. (1)

Để đường thẳng cắt đồ thị tại hai điểm phân biệt A, B thì phương trình (1) có hai nghiệm phân biệt, do đó ∆ = (m – 2)² – 4(m – 2) > 0 ⇔ \(\left[ \begin{array}{l}m > 6\\m < 2\end{array} \right.\).

Khi đó, đường thẳng cắt đồ thị tại hai điểm phân biệt A(x₁; x₁ + m – 1) và

B(x₂; x₂ + m – 1) với x₁, x₂ là hai nghiệm phân biệt của phương trình (1).

Theo định lí Viète, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2--m\\{x_1}.{x_2} = m - 2\end{array} \right.\).

Ta có: AB = \(2\sqrt 3 \).

⇔ \(\sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left[ {\left( {{x_1} + m - 1} \right) - \left( {{x_2} + m - 1} \right)} \right]}^2}} = 2\sqrt 3 \)

⇔ (x₁ – x₂)² + [(x₁ + m – 1) – (x₂ + m – 1)]² = 12

⇔ 2(x₁ – x₂)² = 12

⇔ (x₁ – x₂)² = 6

⇔ (x₁ + x₂)² – 4x₁x₂ = 6

⇔ (2 – m)² – 4(m – 2) = 6

⇔ m² – 8m + 6 = 0

⇔ m = 4 ± \(\sqrt {10} \) (thỏa mãn).

Câu 5/45

Cho hàm số y = \(\frac{{{x^2} - 2x + 1}}{{x + 1}}\) có đồ thị (C). Khẳng định nào sau đây là sai?

A. Đường thẳng x = −1 là tiệm cận đứng của đồ thị (C).

B. Đường thẳng y = 1 là tiệm cận ngang của đồ thị (C).

C. Đường thẳng y = x – 3 là tiệm cận xiên của đồ thị (C).

D. Hàm số có hai cực trị.

Lời giải

Đáp án đúng là: B

Ta thấy \(\mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} - 2x + 1}}{{x + 1}} = + \infty \), \(\mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} - 2x + 1}}{{x + 1}} = - \infty \).

Do đó, đồ thị hàm số không có tiệm cận ngang.

Câu 6/45

Cho f(x) là một hàm số liên tục trên đoạn [a; b] và F(x) là một nguyên hàm của f(x) trên [a; b]. Khi đó \(\int\limits_a^b {f\left( x \right)dx} \)có giá trị bằng

A. F(b) – F(a).

B. F(b) – F(a) + C; C là hằng số.

C. F(a) – F(b).

D. F(a) – F(b) + C; C là hằng số.

Lời giải

Đáp án đúng là: A

Theo định nghĩa tích phân, ta có: \(\int\limits_a^b {f\left( x \right)dx} \) = F(b) – F(a).

Câu 7/45

Phát biểu nào sau đây là sai?

A. \(\int {dx} \) = x + C.

B. \(\int {{x^3}dx} = \frac{1}{4}{x^4}\) + C.

C. \(\int {\frac{1}{x}} dx\) = lnx + C.

D. \(\int {{e^x}} dx\) = e^x + C.

Lời giải

Đáp án đúng là: C

Ta có: \(\int {\frac{1}{x}} dx\) = ln\(\left| x \right|\) + C.

Câu 8/45

Nguyên hàm F(x) của hàm số f(x) = 4x³ + 2x – 1 thỏa mãn F(1) = 10.

A. F(x) = x⁴ + x² + 1.

B. F(x) = x⁴ – x² + 10.

C. F(x) = x⁴ + x² – x + 9.

D. F(x) = x⁴ + x² – x + 10.

Lời giải

Đáp án đúng là: C

Ta có: F(x) = \(\int {f\left( x \right)dx = \int {\left( {4{x^3} + 2x - 1} \right)dx} } \) = x⁴ + x² – x + C.

Mà F(1) = 10 ⇔ 1⁴ + 1² – 1 + C = 10 ⇔ C = 9.

Vậy F(x) = x⁴ + x² – x + 9.

Câu 9/45