Giải SGK Toán 12 KNTT Bài 15. Phương trình đường thẳng trong không gian có đáp án
60 người thi tuần này 4.6 1.1 K lượt thi 29 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Sau khi học xong bài này, ta giải quyết bài toán này như sau:
Ta có \(\overrightarrow {MN} = \left( { - 3; - 3;12} \right) = - 3\left( {1;1; - 4} \right)\)
Đường thẳng MN đi qua điểm M(2; 3; −4) và có một vectơ chỉ phương \(\overrightarrow u = \left( {1;1; - 4} \right)\) có phương trình là: \(\left\{ \begin{array}{l}x = 2 + t\\y = 3 + t\\z = - 4 - 4t\end{array} \right.\).
Mặt phẳng Oxy có phương trình là z = 0.
Gọi D là giao điểm của đường thẳng MN với mặt phẳng Oxy nên tọa độ điểm D là nghiệm của hệ \(\left\{ \begin{array}{l}x = 2 + t\\y = 3 + t\\z = - 4 - 4t\\z = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\\z = 0\\t = - 1\end{array} \right.\). Vậy D(1; 2; 0).
Ta có \(MD = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 1} \right)}^2} + {4^2}} = \sqrt {18} \); \(MN = \sqrt {{{\left( { - 3} \right)}^2} + {{\left( { - 3} \right)}^2} + {{12}^2}} = \sqrt {162} \).
Vì MD < MN nên D nằm giữa M và N.
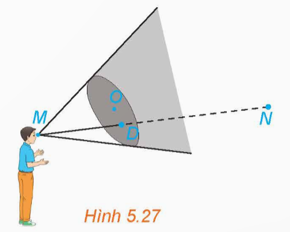
Vậy tấm bìa có che khuất tầm nhìn của người quan sát đối với vật đặt ở điểm N.
Lời giải
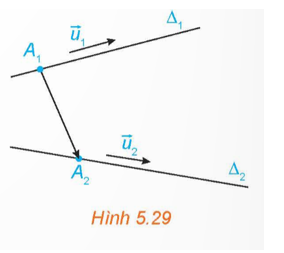
a) Trong không gian thì có vô số đường thẳng đi qua M và vuông góc với giá của nên khẳng định này sai.
b) Qua M có duy nhất một đường thẳng đi qua M và song song hoặc trùng với giá của cho trước. Do đó khẳng định này đúng.
Lời giải
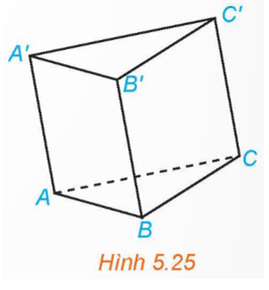
Những vectơ chỉ phương của đường thẳng AB là: \(\overrightarrow {AB} ,\overrightarrow {BA} ,\overrightarrow {A'B'} ,\overrightarrow {B'A'} \).
Lời giải
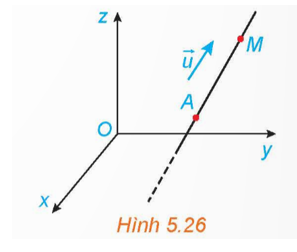
a) Một vật thể chuyển động với vectơ vận tốc không đổi \(\overrightarrow u = \left( {a;b;c} \right) \ne \overrightarrow 0 \) và xuất phát từ điểm A(x0; y0; z0). Vectơ vận tốc này chính là vectơ chỉ phương của đường thẳng mà vật thể chuyển động.
Do đó đường thẳng này đi qua điểm A(x0; y0; z0) và có vectơ chỉ phương là \(\overrightarrow u = \left( {a;b;c} \right).\)
b) Ta có \(\overrightarrow {MA} = \left( {x - {x_0};y - {y_0};z - {z_0}} \right)\).
Khi đó ta có \(\overrightarrow {MA} \) cùng phương với \(\overrightarrow u \).
Suy ra \(\overrightarrow {MA} = t\overrightarrow u \)\( \Leftrightarrow \left\{ \begin{array}{l}x - {x_0} = ta\\y - {y_0} = tb\\z - {z_0} = tc\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = {x_0} + ta\\y = {y_0} + tb\\z = {z_0} + tc\end{array} \right.,t > 0\).
Lời giải
a) Ta có A(2; 0; 1), B(3; 3; 2) là các điểm thuộc ∆.
Có \(\overrightarrow u = \left( {1;3;1} \right)\) là một vectơ chỉ phương của ∆.
b) Phương trình tham số của đường thẳng đi qua gốc tọa độ O(0; 0; 0) và có vectơ chỉ phương \(\overrightarrow v = \left( {1;3;1} \right)\) là \(\left\{ \begin{array}{l}x = t\\y = 3t\\z = t\end{array} \right.\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.