Giải SBT Toán 12 Tập 1 KNTT Bài 8. Biểu thức tọa độ của các phép toán vectơ có đáp án

a) Ta có: \(\overrightarrow a - \overrightarrow b \) = (3 – 2;0 – 7;4 – 7) = (1; −7; −3).

Do đó, \(\overrightarrow a - \overrightarrow b + \overrightarrow c \) = (1 + 2; −7 + 7; −3 + 2) = (3; 0; −1).

Vậy \(\overrightarrow a - \overrightarrow b + \overrightarrow c \) = (3; 0; −1).

Ta có: 2\(\overrightarrow a \) = (6; 0; 8), \(3\overrightarrow b \) = (6; 21; 21), \(4\overrightarrow c \) = (8; 28; 8).

Do đó, \(2\overrightarrow a + 3\overrightarrow b - 4\overrightarrow c \) = (4; −7; 21).

b) Ta có: −\(\overrightarrow a \) = (−3; 0; −4).

Do đó, \(\left( { - \overrightarrow a } \right).\overrightarrow b \) = −3.2 + 0.7 + \(\left( { - 4} \right)\).7 = −34.

Ta có: 3\(\overrightarrow a \) = (9; 0; 12).

Do đó, \(\left( {3\overrightarrow a } \right)\).\(\overrightarrow c \) = 9.2 + 0.7 + 12.2 = 42.

c) Ta có: cos\(\left( {\overrightarrow a ,\overrightarrow b } \right)\) = \(\frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\) = \(\frac{{3.2 + 0.7 + 4.7}}{{\sqrt {{3^2} + {0^2} + {4^2}} .\sqrt {{2^2} + {7^2} + {7^2}} }}\) = \(\frac{{\sqrt {102} }}{{15}}\).

Ta có: cos\(\left( {\overrightarrow a ,\overrightarrow c } \right)\) = \(\frac{{\overrightarrow a .\overrightarrow c }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow c } \right|}}\) = \(\frac{{3.2 + 0.7 + 4.2}}{{\sqrt {{3^2} + {0^2} + {4^2}} .\sqrt {{2^2} + {7^2} + {2^2}} }}\) = \(\frac{{14}}{{5\sqrt {57} }}\).

a) Ta có: \(2\overrightarrow b \) = (2; 4; 6)

Suy ra \(\overrightarrow a - 2\overrightarrow b \) = (m – 2; 3 – 4; 6 – 6) = (m – 2; −1; 0).

Mà \(\overrightarrow a - 2\overrightarrow b \) = (3; −1; 0) = (m – 2; −1; 0).

Do đó, m – 2 = 3 hay m = 5.

b) Ta có: \(\overrightarrow a .\overrightarrow b \) = m.1 + 3.2 + 6.3 = m + 24 = 10

Suy ra m = −14.

c) Ta có: \(\left| {\overrightarrow a } \right|\) = \(\sqrt {{m^2} + {3^2} + {6^2}} = 9\)

                ⇒ \(\sqrt {{m^2} + 45} = 9\)

                ⇒ m² + 45 = 81

                ⇒ m² = 36

                ⇒ m = ±6.

a) Gọi I(x; y; z)

Ta có: I là trọng tâm tam giác ABC nên \(\left\{ \begin{array}{l}x = \frac{{1 + 2 + 6}}{3}\\y = \frac{{3 + 0 + 9}}{3}\\z = \frac{{ - 3 + 5 + ( - 5)}}{3}\end{array} \right.\) ⇔ \(\left\{ \begin{array}{l}x = 3\\y = 4\\z =  - 1\end{array} \right.\).

Vậy I(3; 4; −1).

b) Gọi G(x0; y0; z0), theo đề ta có: DG = 3IG nên DG = \(\frac{3}{4}\)DI suy ra \[\overrightarrow {DG}  = \frac{3}{4}\overrightarrow {DI} \].

Suy ra \(\left\{ \begin{array}{l}{x_0} + 1 = \frac{3}{4}.4\\{y_0} + 4 = \frac{3}{4}.8\\{z_0} - 3 = \frac{3}{4}.( - 4)\end{array} \right.\) ⇒ \(\left\{ \begin{array}{l}{x_0} = 2\\{y_0} = 2\\{z_0} = 0\end{array} \right.\).

Vậy G(2; 2; 0).

Ta có: \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)

\(\overrightarrow {OA} - \overrightarrow {OG} + \overrightarrow {OB} - \overrightarrow {OG} + \overrightarrow {OC} - \overrightarrow {OG} + \overrightarrow {OD} - \overrightarrow {OG} = \overrightarrow 0 \)

\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} - 4\overrightarrow {OG} = \overrightarrow 0 \)

\(\frac{1}{4}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right) = \overrightarrow {OG} \)

Do đó, \(\overrightarrow {OG} = \frac{1}{4}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right)\).

Vậy từ đây, với biểu thức tọa độ của phép cộng vectơ và phép nhân một số với một vectơ ta được:

x_G = \(\frac{{{x_A} + {x_B} + {x_C} + {x_D}}}{4}\);

y_G = \(\frac{{{y_A} + {y_B} + {y_C} + {y_D}}}{4}\);

z_G = \(\frac{{{z_A} + {z_B} + {z_C} + {z_D}}}{4}\).

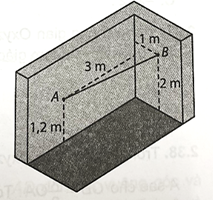
Ta có: AB = \(\sqrt {{{\left( {0 - 3} \right)}^2} + {{\left( {6 - 5} \right)}^2} + {{\left( {2 - 2} \right)}^2}} \) = \(\sqrt {10} \);

           AC = \(\sqrt {{{\left( {3 - 2} \right)}^2} + {{\left( {5 - 3} \right)}^2} + {{\left( {2 - 6} \right)}^2}} \) = \(\sqrt {21} \);

           BC = \(\sqrt {{{\left( {0 - 2} \right)}^2} + {{\left( {6 - 3} \right)}^2} + {{\left( {2 - 6} \right)}^2}} \) = \(\sqrt {29} \).

   cos\(\widehat {BAC}\) = cos\(\left( {\overrightarrow {AC} ,\overrightarrow {AB} } \right)\) = \(\frac{{\overrightarrow {AC} .\overrightarrow {AB} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}}\) = \(\frac{{ - 3.( - 1) + 1.( - 2) + 0.4}}{{\sqrt {10} .\sqrt {21} }}\) = \(\frac{1}{{\sqrt {210} }}\).

Suy ra \(\widehat {BAC}\) ≈ 86°.

    cos\(\widehat {ABC}\) = cos \(\left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right)\) = \(\frac{{\overrightarrow {BC} .\overrightarrow {BA} }}{{\left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|}}\) = \(\frac{{3.2 + ( - 1).( - 3) + 0.4}}{{\sqrt {10} .\sqrt {29} }}\) = \(\frac{9}{{\sqrt {290} }}\).

Suy ra \(\widehat {ABC}\) ≈ 58°.

Từ đây, \(\widehat {ACB}\) = 180° − 86° − 58° = 36°.

a) Ta có: C'(0; 0; 0), D'(0; 1; 0), B'(1; 0; 0); C(0; 0; 1); D(0; 1; 1).

Ta có: \(\overrightarrow {CC'} = \overrightarrow {AA'} = \overrightarrow {BB'} = \overrightarrow {DD'} \) = (0; 0; −1).

Gọi B(x; y; z), ta có: \(\left\{ \begin{array}{l}1 - x = 0\\0 - y = 0\\0 - z = - 1\end{array} \right.\)⇔ \(\left\{ \begin{array}{l}x = 1\\y = 0\\z = 1\end{array} \right.\).

Vậy B(1; 0; 1).

Ta có: \(\overrightarrow {AB} = \overrightarrow {DC} \) ⇒ A(1; 1; 1).

           \(\overrightarrow {CC'} = \overrightarrow {AA'} \)⇒ A' (1; 1; 0).

b) Gọi G(x_G; y_G; z_G), ta có:

\(\left\{ \begin{array}{l}{x_G} = \frac{{1 + 0 + 0}}{3} = \frac{1}{3}\\{y_G} = \frac{{0 + 1 + 0}}{3} = \frac{1}{3}\\{z_G} = \frac{{0 + 0 + 1}}{3} = \frac{1}{3}\end{array} \right.\).

Vậy G\(\left( {\frac{1}{3};\frac{1}{3};\frac{1}{3}} \right)\).

c) Ta có: \(\overrightarrow {OG} = \left( {\frac{1}{3};\frac{1}{3};\frac{1}{3}} \right)\), \(\overrightarrow {OA} = (1;1;1).\)

Có \(\overrightarrow {OG} = \frac{1}{3}\overrightarrow {OA} \) nên ba điểm O, G, A thẳng hàng.