Trên sân thể dục thầy giáo dựng hai chiếc cột vuông góc với mặt sân, chiều cao của mỗi chiếc cột lần lượt là 3 m và 2 m. Xét hệ tọa độ Oxyz sao cho mặt phẳng (Oxy) trùng với mặt sân, trục Oz hướng thẳng đứng lên trời. Đơn vị trong hệ tọa độ Oxyz được lấy theo mét.
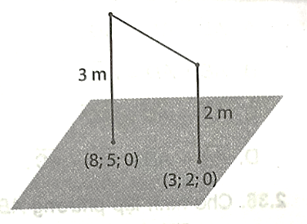
a) Biết rằng chân của hai cột đó có tọa độ lần lượt là (8; 5; 0) và (3; 2; 0), hãy tìm tọa độ điểm đầu của mỗi cột.
b) Thầy giáo dự định căng một sợi dây nối hai đầu của hai cột. Hỏi sợi dây cần có độ dài tối thiểu là khoảng bao nhiêu mét?
Trên sân thể dục thầy giáo dựng hai chiếc cột vuông góc với mặt sân, chiều cao của mỗi chiếc cột lần lượt là 3 m và 2 m. Xét hệ tọa độ Oxyz sao cho mặt phẳng (Oxy) trùng với mặt sân, trục Oz hướng thẳng đứng lên trời. Đơn vị trong hệ tọa độ Oxyz được lấy theo mét.
a) Biết rằng chân của hai cột đó có tọa độ lần lượt là (8; 5; 0) và (3; 2; 0), hãy tìm tọa độ điểm đầu của mỗi cột.
b) Thầy giáo dự định căng một sợi dây nối hai đầu của hai cột. Hỏi sợi dây cần có độ dài tối thiểu là khoảng bao nhiêu mét?
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Ta thấy đầu chiếc cột có độ cao 3 m có tọa độ là (8; 5; 3), đầu chiếc cột có độ cao 2 m có tọa độ là (3; 2; 2).
b) Khoảng cách giữa hai đầu sợi dây của chiếc cột là:
\(\sqrt {{{\left( {8 - 3} \right)}^2} + {{\left( {5 - 2} \right)}^2} + {{\left( {3 - 2} \right)}^2}} \) ≈ 5,92 (m).
Vậy sợi dây cần có độ dài tối thiểu 5,92 m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
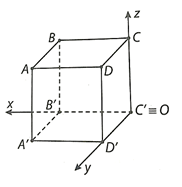
a) Ta có: C'(0; 0; 0), D'(0; 1; 0), B'(1; 0; 0); C(0; 0; 1); D(0; 1; 1).
Ta có: \(\overrightarrow {CC'} = \overrightarrow {AA'} = \overrightarrow {BB'} = \overrightarrow {DD'} \) = (0; 0; −1).
Gọi B(x; y; z), ta có: \(\left\{ \begin{array}{l}1 - x = 0\\0 - y = 0\\0 - z = - 1\end{array} \right.\)⇔ \(\left\{ \begin{array}{l}x = 1\\y = 0\\z = 1\end{array} \right.\).
Vậy B(1; 0; 1).
Ta có: \(\overrightarrow {AB} = \overrightarrow {DC} \) ⇒ A(1; 1; 1).
\(\overrightarrow {CC'} = \overrightarrow {AA'} \)⇒ A' (1; 1; 0).
b) Gọi G(xG; yG; zG), ta có:
\(\left\{ \begin{array}{l}{x_G} = \frac{{1 + 0 + 0}}{3} = \frac{1}{3}\\{y_G} = \frac{{0 + 1 + 0}}{3} = \frac{1}{3}\\{z_G} = \frac{{0 + 0 + 1}}{3} = \frac{1}{3}\end{array} \right.\).
Vậy G\(\left( {\frac{1}{3};\frac{1}{3};\frac{1}{3}} \right)\).
c) Ta có: \(\overrightarrow {OG} = \left( {\frac{1}{3};\frac{1}{3};\frac{1}{3}} \right)\), \(\overrightarrow {OA} = (1;1;1).\)
Có \(\overrightarrow {OG} = \frac{1}{3}\overrightarrow {OA} \) nên ba điểm O, G, A thẳng hàng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
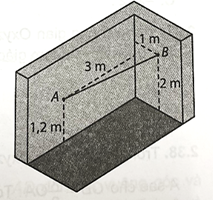
a) Chọn hệ trục Oxyz như hình bên.
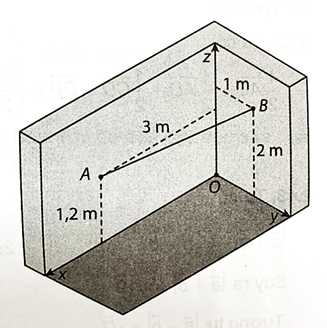
Khi đó tọa độ của hai đầu dây A, B là A(3; 0; 1,2) và B(0; 1; 2).
b) Độ dài của sợi dây là:
AB = \(\sqrt {{{\left( {0 - 3} \right)}^2} + \left( {1 - 0} \right){}^2 + {{\left( {2 - 1,2} \right)}^2}} \) ≈ 3,26 (m).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập