Câu hỏi:
13/07/2024 22,342
Khối chỏm cầu có bán kính R và chiều cao h (0 < h ≤ R) sinh ra khi quay hình phẳng giới hạn bởi cung tròn có phương trình , trục hoành và hai đường thẳng x = R – h, x = R xung quanh trục Ox (H.4.30). Tính thể tích của khối chỏm cầu này.
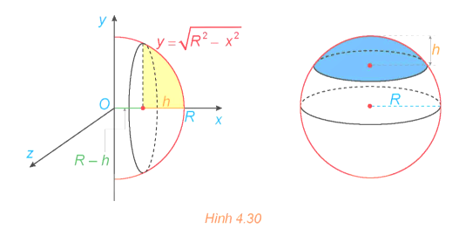
Khối chỏm cầu có bán kính R và chiều cao h (0 < h ≤ R) sinh ra khi quay hình phẳng giới hạn bởi cung tròn có phương trình , trục hoành và hai đường thẳng x = R – h, x = R xung quanh trục Ox (H.4.30). Tính thể tích của khối chỏm cầu này.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Thể tích cần tìm là:
\(V = \pi \int\limits_{R - h}^R {\left( {{R^2} - {x^2}} \right)dx} \)\( = \pi \left. {\left( {{R^2}x - \frac{{{x^3}}}{3}} \right)} \right|_{R - h}^R\)
\( = \pi \left( {{R^3} - \frac{{{R^3}}}{3} - {R^2}\left( {R - h} \right) + \frac{{{{\left( {R - h} \right)}^3}}}{3}} \right)\)\( = \pi \left( {{R^3} - \frac{{{R^3}}}{3} - {R^3} + {R^2}h + \frac{{{R^3}}}{3} - {R^2}h + R{h^2} - \frac{{{h^3}}}{3}} \right)\)
\( = \pi \left( {R{h^2} - \frac{{{h^3}}}{3}} \right)\)\( = \pi {h^2}\left( {R - \frac{h}{3}} \right)\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
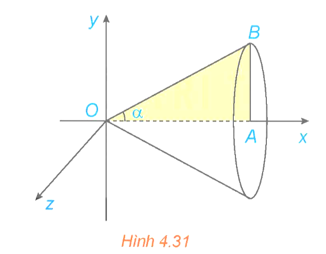
a) Xét tam giác OAB vuông tại A, có AB = OA.tanα = a.tanα.
Khi quay miền tam giác OAB xung quanh trục Ox ta được khối nón có bán kính đáy r = AB = a.tanα và chiều cao h = OA = a.
Do đó \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {a^3}{\tan ^2}\alpha \).
b) Có \(V' = \frac{1}{3}\pi {a^3}.2\tan \alpha .\frac{1}{{{{\cos }^2}\alpha }}\).
Vì \(0 < \alpha \le \frac{\pi }{4}\) Þ 0 < tanα ≤ 1 nên V' > 0. Do đó V là hàm số đồng biến trên \(\left( {0;\frac{\pi }{4}} \right)\).
Do đó \(\mathop {\max }\limits_{\left( {0;\frac{\pi }{4}} \right]} V = V\left( {\frac{\pi }{4}} \right) = \frac{1}{3}\pi {a^3}\).
Vậy \(\alpha = \frac{\pi }{4}\) thì thể tích khối nón là lớn nhất.
Lời giải
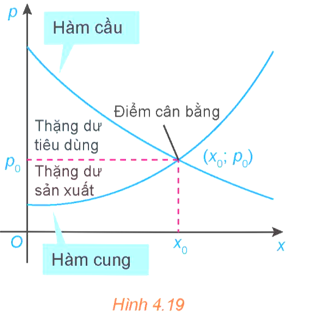
Sự bất bình đẳng thu nhập của Hoa Kỳ vào năm 2005 là:
\(S = \int\limits_0^{100} {\left| {{{\left( {0,00061{x^2} + 0,0218x + 1723} \right)}^2} - x} \right|dx} \)
\( = \int\limits_0^{100} {\left| {\left( {{{0,00061}^2}{x^4} + {{4,7524.10}^{ - 4}}{x^2} + {{1723}^2} + {{2,6596.10}^{ - 5}}{x^3} + 2,10206{x^2} + 75,1228x} \right) - x} \right|dx} \)
\( = \int\limits_0^{100} {\left| {\left( {{{0,00061}^2}{x^4} + {{2,6596.10}^{ - 5}}{x^3} + 2,10253524{x^2} + 74,1228x + {{1723}^2}} \right)} \right|dx} \)
\( = \int\limits_0^{100} {\left( {{{0,00061}^2}{x^4} + {{2,6596.10}^{ - 5}}{x^3} + 2,10253524{x^2} + 74,1228x + {{1723}^2}} \right)dx} \)
\[ = \left. {\left( {{{7,442.10}^{ - 8}}.{x^5} + {{6,649.10}^{ - 6}}.{x^4} + 0,70084508.{x^3} + 37,0614.{x^2} + {{1723}^2}.x} \right)} \right|_0^{100}\]
\[ = {7,442.10^{ - 8}}{.100^5} + {6,649.10^{ - 6}}{.100^4} + {0,70084508.100^3} + {37,0614.100^2} + {1723^2}.100\]
= 297945768,2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận