Một công ty ước tính rằng chi phí C (USD) để sản xuất x đơn vị sản phẩm có thể được mô hình hóa bằng công thức
C = 800 + 0,04x + 0,0002x2.
Tìm mức sản xuất sao cho chi phí trung bình \(\overline C (x) = \frac{{C(x)}}{x}\) cho mỗi đơn vị hàng hóa là nhỏ nhất.
Một công ty ước tính rằng chi phí C (USD) để sản xuất x đơn vị sản phẩm có thể được mô hình hóa bằng công thức
C = 800 + 0,04x + 0,0002x2.
Tìm mức sản xuất sao cho chi phí trung bình \(\overline C (x) = \frac{{C(x)}}{x}\) cho mỗi đơn vị hàng hóa là nhỏ nhất.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có: \(\overline C (x) = \frac{{C(x)}}{x} = \frac{{800}}{x} + 0,04 + 0,0002x\)
Suy ra, \(\overline {C'} (x) = - \frac{{800}}{{{x^2}}} + 0,0002 = \frac{{0,0002{x^2} - 800}}{{{x^2}}}\)
\(\overline {C'} (x)\) = 0 ⇔ x = 2 000 (do x > 0).
Bảng biến thiên của hàm số:
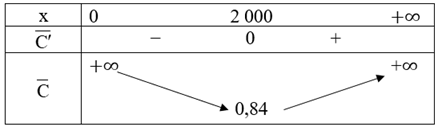
Từ bảng biến thiên suy ta với mức sản xuất là 2 000 thì chi phí trung bình cho mỗi đơn vị hàng hóa là nhỏ nhất.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta có: R'(x) = \(\frac{{5000}}{{1 + 5{e^{ - x}}}}\), x ≥ 0.
R''(x) = \(\frac{{ - 25000{e^{ - x}}{{\left( {1 + 5{e^{ - x}}} \right)}^2} + 25000{e^{ - x}}.2\left( {1 + 5{e^{ - x}}} \right).5{e^{ - x}}}}{{{{\left( {1 + 5{e^{ - x}}} \right)}^4}}}\)
R''(x) = 0 ⇔ x = ln5 ≈ 1,61.
Ta có bảng biến thiên như sau:
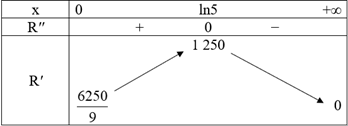
Từ bảng biến thiên, ta thấy tốc độ bán hàng đạt tối đa vào thời điểm năm thứ hai.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi x (m) là cạnh đáy của chiếc hộp.
Khi đó, ta có chiều cao của chiếc hộp là \(\frac{{2000}}{{{x^2}}}\) (cm).
Suy ra, tổng diện tích bề mặt của chiếc hộp là:
S = 2x2 + 4x.\(\frac{{2000}}{{{x^2}}}\) = 2x2 + \(\frac{{8000}}{x}\), x > 0.
Ta có: S' = 4x – \(\frac{{8000}}{{{x^2}}}\) = \(\frac{{4{x^3} - 8000}}{{{x^2}}}\)
S' = 0 ⇔ x = 10\(\sqrt[3]{2}\).
Ta có bảng biến thiên:
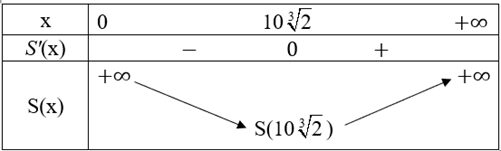
Dễ thấy lượng vật liệu dùng để sản xuất là nhỏ nhất khi cạnh đáy của hộp là 10\(\sqrt[3]{2}\) (cm) và chiều cao của hộp là \(\frac{{20}}{{\sqrt[3]{4}}}\) cm.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập