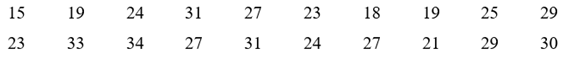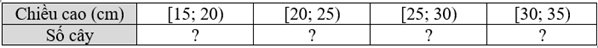Câu hỏi:
21/08/2024 1,290
Cho mẫu số liệu ghép nhóm sau về thời gian ngủ trong ngày của các học sinh lớp 12A.
Tính số trung bình và độ lệch chuẩn cho mẫu số liệu ghép nhóm trên.
Cho mẫu số liệu ghép nhóm sau về thời gian ngủ trong ngày của các học sinh lớp 12A.
Tính số trung bình và độ lệch chuẩn cho mẫu số liệu ghép nhóm trên.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn giá trị đại diện cho mỗi nhóm dố liệu ta có mẫu số liệu sau:
Cỡ mẫu là: 5 + 12 + 15 + 3 = 35.
Số trung bình là:
\(\overrightarrow x \) = \(\frac{1}{{35}}\)(5.6,75 + 12.7,25 + 15.7,75 + 3.8,35) ≈ 7,48.
Độ lệch chuẩn là:
s = \(\sqrt {\frac{1}{{35}}\left( {5.6,{{75}^2} + ... + 3.8,{{25}^2}} \right) - 7,{{48}^2}} \) ≈ 0,39.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn giá trị đại diện cho bảng số liệu, ta có bảng sau:
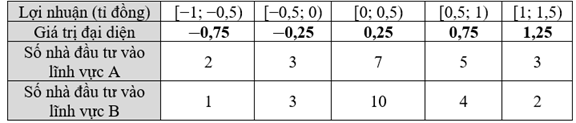
Lợi nhuận trung bình của các nhà đầu tư vào lĩnh vực A là:
\(\overline x = \frac{1}{{20}}\left[ {2.\left( { - 0,75} \right) + 3.\left( { - 0,25} \right) + 7.0,25 + 5.0,75 + 3.1,25} \right]\) = 0,35.
Lợi nhuận trung bình của các nhà đầu tư vào lĩnh vực B là:
\(\overline x = \frac{1}{{20}}\left[ {1.\left( { - 0,75} \right) + 3.\left( { - 0,25} \right) + 10.0,25 + 4.0,75 + 2.1,25} \right]\) = 0,325.
Độ lệch chuẩn của lợi nhuận khi đầu tư vào lĩnh vực A là:
sA = \(\sqrt {\frac{1}{{20}}\left[ {2.{{\left( { - 0,75} \right)}^2} + 3.{{\left( { - 0,25} \right)}^2} + 7.0,{{25}^2} + 5.0,{{75}^2} + 3.1,{{25}^2}} \right] - 0,{{35}^2}} \) ≈ 0,58.
Độ lệch chuẩn của lợi nhuận khi đầu tư vào lĩnh vực B là:
sB = \(\sqrt {\frac{1}{{20}}\left[ {1.{{\left( { - 0,75} \right)}^2} + 3.{{\left( { - 0,25} \right)}^2} + 10.0,{{25}^2} + 4.0,{{75}^2} + 2.1,{{25}^2}} \right] - 0,{{35}^2}} \)≈ 0,48.
Do sA > sB nên đầu tư vào lĩnh vực A rủi ro hơn lĩnh vực B.
Lời giải
a) Tổng chiều cao 20 cây xoan giống đó là:
15 + 19 + 24 + 31 + 27 + 23 + 18 + 19 + 25 + 29 + 23 + 33 + 34 + 27 + 31 + 24 + 27
+ 21 + 29 + 30 = 509.
Chiều cao trung bình của 20 cây xoan giống là: \(\frac{{509}}{{20}}\) = 25,45.
Ta có: Tổng bình phương của 20 giá trị số liệu trong bảng là:
152 + 192 + 242 + 312 + 272 + 232 + 182 + 192 + 252 + 292 + 232 + 332 + 342 + 272 + 312
+ 242 + 272 + 212 + 292 + 302 = 13 483.
Lúc này, độ lệch chuẩn của mẫu số liệu gốc là:
Sg = \(\sqrt {\frac{1}{{20}}.13483 - 25,{{45}^2}} \) ≈ 5,14.
b) Ta có bảng số liệu ghép nhóm như sau:
Ta có bảng giá trị đại diện là:
Số trung bình là:
\(\overline x \) = \(\frac{{4.17,5 + 5.22,5 + 6.27,5 + 5.32,5}}{{20}}\) = 25,5.
Độ lệch chuẩn là:
s = \(\sqrt {\frac{1}{{20}}\left( {4.17,{5^2} + 5.22,{5^2} + 6.27,{5^2} + 5.32,{5^2}} \right) - 25,{5^2}} \) ≈ 5,34.
c) Từ số liệu tính được phần a, b ta nên dùng giá trị sg để đo mức độ phân tán về chiều cao của 20 cây xoan giống.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận