Câu hỏi:
28/08/2024 2,764
Cho hình vuông ABCD và điểm M bất kì trên cạnh BC (M khác B và C). Qua B kẻ đường thẳng vuông góc với DM tại H. Chứng minh BHCD là tứ giác nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác BHCD.
Cho hình vuông ABCD và điểm M bất kì trên cạnh BC (M khác B và C). Qua B kẻ đường thẳng vuông góc với DM tại H. Chứng minh BHCD là tứ giác nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác BHCD.
Quảng cáo
Trả lời:
Giải bởi Vietjack
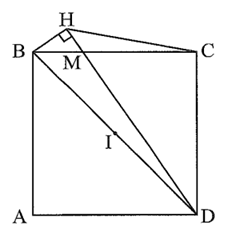
Ta có \(\widehat {BCD} = 90^\circ \) (do ABCD là hình vuông), \(\widehat {BHD} = 90^\circ \) (do BH ⊥ DH).
Khi đó, tam giác BHD vuông tại H và tam giác BCD vuông tại C cùng nội tiếp đường tròn đường kính BD.
Do đó, tứ giác BHCD nội tiếp đường tròn đường kính BD.
Gọi I là trung điểm của BD, khi đó I là tâm của đường tròn ngoại tiếp tứ giác BHCDHot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
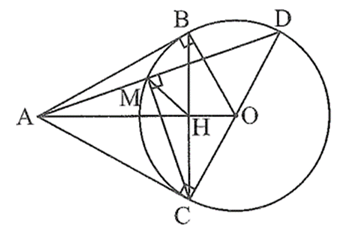
⦁ Ta có: AB = AC (tính chất hai tiếp tuyến cắt nhau) và OA = OB = R.
Suy ra OA là đường trung trực của đoạn thẳng BC, do đó OA ⊥ BC nên \(\widehat {AHC} = 90^\circ .\)
⦁ Ta có \(\widehat {CMD} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn (O) đường kính CD), suy ra \(\widehat {AMC} = 90^\circ .\)
Khi đó, tam giác AMC vuông tại M và tam giác AHC vuông tại H cùng nội tiếp đường tròn đường kính AC.
Do đó, tứ giác AMHC nội tiếp đường tròn đường kính AC.
Lời giải
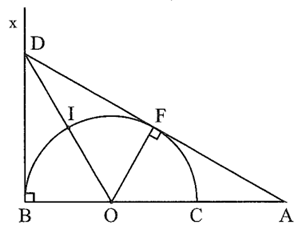
Gọi I là trung điểm của DO.
Ta có BD và AD là tiếp tuyến của đường tròn (O; R) nên \(\widehat {DBO} = 90^\circ \) và \(\widehat {DFO} = 90^\circ .\)
Tam giác DBO vuông tại O nên tam giác này nội tiếp đường tròn tâm I, bán kính bằng \(\frac{1}{2}DO.\)
Tương tự, tam giác DFO vuông tại F nên nội tiếp đường tròn tâm I, bán kính bằng \(\frac{1}{2}DO.\)
Do đó, tứ giác OBDF nội tiếp đường tròn tâm I, bán kính bằng \(\frac{1}{2}DO.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận