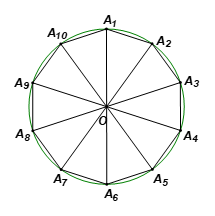
⦁ Các điểm A₁, A₂, A₃, …, A₁₀ chia đường tròn thành 10 cung bằng nhau, mỗi cung có số đo bằng \(\frac{{360^\circ }}{{10}} = 36^\circ ,\) do dó \(\widehat {{A_1}O{A_2}} = \widehat {{A_2}O{A_3}} = ... = \widehat {{A_{10}}O{A_1}} = 36^\circ .\)

Xét ∆OA₁A₂ và ∆OA₂A₃ có:

OA₁ = OA₂; \(\widehat {{A_1}O{A_2}} = \widehat {{A_2}O{A_3}};\) OA₂ = OA₃

Do đó ∆OA₁A₂ = ∆OA₂A₃ (c.g.c).

Suy ra A₁A₂ = A₂A₃ (hai cạnh tương ứng).

Chứng minh tương tự, ta có 10 tam giác cân OA₁A₂, OA₂A₃,…, OA₁₀A₁ bằng nhau vì cùng có hai cạnh bằng R và góc ở đỉnh bằng 36°, suy ra A₁A₂ = A₂A₃ = … = A₁₀A₁ nên đa giác có các cạnh bằng nhau.

⦁ Xét ∆OA₁A₂ cân tại O (do OA₁ = OA₂) nên

\(\widehat {O{A_1}{A_2}} = \widehat {O{A_2}{A_1}} = \frac{{180^\circ - \widehat {{A_1}O{A_2}}}}{2} = \frac{{180^\circ - 36^\circ }}{2} = 72^\circ .\)

Tương tự, ta cũng có ∆OA₂A₃ cân tại O (do OA₂ = OA₃) nên

\[\widehat {O{A_2}{A_3}} = \widehat {O{A_3}{A_2}} = \frac{{180^\circ - \widehat {{A_2}O{A_3}}}}{2} = \frac{{180^\circ - 36^\circ }}{2} = 72^\circ .\]

Suy ra \(\widehat {{A_1}{A_2}{A_3}} = \widehat {O{A_2}{A_1}} + \widehat {O{A_2}{A_3}} = 72^\circ + 72^\circ = 144^\circ .\)

Do đó ta tính được mỗi góc của đa giác A₁A₂A₃…A₁₀ bằng 144°.

Vậy đa giác A₁A₂A₃... A₁₀ có các cạnh bằng nhau và các góc bằng nhau nên là một đa giác đều.

Câu 2/6

Các hình phẳng đều có trong Hình 10 cho ta hình ảnh của đa giác đều nào? Tính số đo góc của đa giác đều đó.

Xem đáp án

Lời giải

Các hình phẳng đều có trong Hình 10 cho ta hình ảnh của lục giác đều.

Tổng số đo mỗi góc của hình lục giác đều bằng tổng số đo của hai tứ giác và bằng 2.360° = 720°.

Mà các góc của lục giác đều có số đo bằng nhau nên số đo mỗi góc của lục giác đều bằng \[\frac{{720^\circ }}{6} = 120^\circ .\]

Câu 3/6

Dựa trên gợi ý của hình ngũ giác đều (Hình 11a), tìm phép quay biến hình con sao biển thành chính nó (Hình 11b).

Xem đáp án

Lời giải

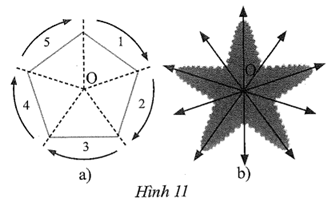
Ta thấy hình con sao biển là hình phẳng đều tương tự ngũ giác đều tâm O.

Các phép quay biến hình con sao biển thành chính nó là phép quay 72°, 144°, 216°, 288° hoặc 360° tâm O cùng chiều hoặc ngược chiều kim đồng hồ.

Câu 4/6

Ngũ giác đài hay Lầu năm góc là trụ sở Bộ Quốc phòng Hoa Kỳ có dạng hình ngũ giác đều với độ dài cạnh khoảng 280 m như Hình 12. Tính khoảng cách từ tâm đối xứng đến một cạnh của ngũ giác đều này (kết quả làm tròn đến hàng phần mười của mét).

(Nguồn: https://khoahoc. tv/ ngu-giac-dai-lau-nam-goc-6515)

Xem đáp án

Lời giải

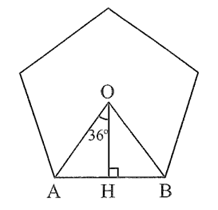
Ngũ giác đài hay Lầu năm góc là trụ sở Bộ Quốc phòng Hoa Kỳ có dạng hình ngũ giác đều với độ dài cạnh khoảng 280 m như Hình 12. Tính khoảng cách (ảnh 1)

Gọi O là tâm đối xứng, AB là cạnh của ngũ giác đều. Kẻ OH ⊥ AB tại H.

Vì ngũ giác đã cho là ngũ giác đều nên nội tiếp đường tròn (O; OA) và các đỉnh của ngũ giác đều chia đường tròn thành 5 cung bằng nhau, do đó \(\widehat {AOB} = \frac{{360^\circ }}{5} = 72^\circ .\)

Xét ∆OAB cân tại O (do OA = OB) nên đường cao OH đồng thời là đường phân giác, đường trung tuyến của tam giác.

Suy ra \(\widehat {AOH} = \frac{{\widehat {AOB}}}{2} = 36^\circ \) và H là trung điểm của AB nên \(AH = \frac{{AB}}{2} = \frac{{280}}{2} = 140\;\) (m).

Xét ∆OAH vuông tại H, ta có:

OH = AH . cot 36° = 140 . cot 36° ≈ 192,7 (m).

Câu 5/6

Cho hình vuông ABCD cạnh a có O là giao điểm của hai đường chéo. Chứng minh có đường tròn (O; R) đi qua các đỉnh của hình vuông và có đường tròn (O; r) tiếp xúc với các cạnh của hình vuông. Tính theo a bán kính R và r.

Xem đáp án

Lời giải

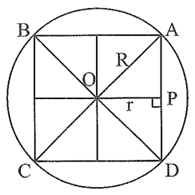
Cho hình vuông ABCD cạnh a có O là giao điểm của hai đường chéo. Chứng minh có đường tròn (O; R) đi qua các đỉnh của hình vuông và có đường tròn (O; r) tiếp xúc với các cạnh của hình vuông. Tính theo a bán kính R và r. (ảnh 1)

⦁ Vì ABCD là hình vuông nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường. Do đó OA = OB = OC = OD và AC ⊥ BD.

Vì ABCD là hình vuông ABCD nên nó nội tiếp đường tròn (O; R) với bán kính là \(R = OA = OB = OC = OD = \frac{{a\sqrt 2 }}{2}.\)

⦁ Trong tam giác AOD vuông cân tại O (do OA = OD và \(\widehat {AOD} = 90^\circ \)), vẽ đường cao OP, khi đó OP cũng đồng thời là đường trung tuyến của tam giác AOD.

Do đó \(OP = \frac{{AD}}{2} = \frac{a}{2}\) (tính chất đường trung tuyến ứng với cạnh huyền).

Tương tự, ta có điểm O cách đều các cạnh của hình vuông một khoảng \(\frac{a}{2}.\)

Do đó, đường tròn (O; r) với \(r = \frac{a}{2}\) tiếp xúc với các cạnh của hình vuông ABCD.

Câu 6/6

Hình ảnh những bông hoa dưới đây là hình phẳng đều tương tự các đa giác đều nào?

Xem đáp án

Lời giải

Hình 13a: Hình ảnh bông hoa là hình phẳng đều tương tự tứ giác đều (hình vuông);

Hình 13b: Hình ảnh bông hoa là hình phẳng đều tương tự lục giác đều;

Hình 13c: Hình ảnh bông hoa là hình phẳng đều tương tự ngũ giác đều;

Hình 13d: Hình ảnh bông hoa là hình phẳng đều tương tự bát giác đều.

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

Cho đường tròn (O; R). Lấy các điểm A₁, A₂, A₂, …, A₁₀ trên đường tròn (O; R) sao cho các điểm này chia đường tròn thành 10 cung có số đo bằng nhau. Chứng minh đa giác A₁A₂ A₃…A₁₀ là một đa giác đều.