Giải SBT Toán 9 Chân trời sáng tạo Bài 2. Bảng tần số tương đối và biểu đồ tần số tương đối có đáp án

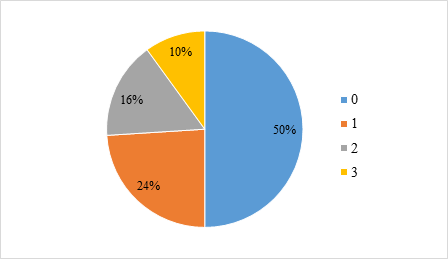
a) Mẫu số liệu thống kê có N = 50 và có 4 giá trị khác nhau là: 0; 1; 2; 3.

Các giá trị 0; 1; 2; 3 có tần số tương đối lần lượt là:

\({f_0} = \frac{{25}}{{50}} \cdot 100\% = 50\% ;\) \({f_1} = \frac{{12}}{{50}} \cdot 100\% = 24\% ;\)

\({f_2} = \frac{8}{{50}} \cdot 100\% = 16\% ;\) \({f_3} = \frac{5}{{50}} \cdot 100\% = 10\% .\)

Bảng tần số tương đối của mẫu số liệu:

b) Số đo cung tròn tương ứng với các hình quạt tròn biểu diễn tần số tương đối của các giá trị như sau:

Ta vẽ được biểu đồ hình quạt tròn:

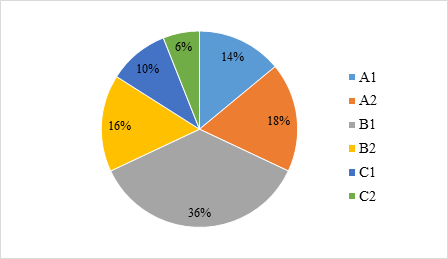
a) Từ biểu đồ hình quạt tròn, ta thấy phần lớn nhân viên của công ty đạt trình độ ngoại ngữ B1 (chiếm 36% tổng số nhân viên công ty).

b) Mẫu số liệu thống kê có N = 150.

Gọi m₁, m₂, m₃, m₄, m₅, m₆ lần lượt là số lượng nhân viên đạt chuẩn trình độ A1, A2, B1, B2, C1, C2.

Ta có:

\({m_1} = 150 \cdot \frac{{14}}{{100}} = 21;\,\,{m_2} = 150 \cdot \frac{{18}}{{100}} = 27;\,\,{m_3} = 150 \cdot \frac{{36}}{{100}} = 54;\)

\({m_4} = 150 \cdot \frac{{16}}{{100}} = 24;\,\,{m_5} = 150 \cdot \frac{{10}}{{100}} = 15;\,\,{m_6} = 150 \cdot \frac{6}{{100}} = 9.\)

Bảng tần số của mẫu số liệu:

a) Số công nhân của phân xưởng trong tháng 10 là:

20 + 10 + 6 + 2 + 2 = 40 (công nhân).

Số công nhân của phân xưởng trong tháng 11 là:

28 + 8 + 4 + 0 + 0 = 40 (công nhân).

Vậy số công nhân của phân xưởng trong tháng 10 và tháng 11 đều là N = 40.

⦁ Gọi f₀, f₁, f₂, f₃, f₄ lần lượt là tần số tương đối của số ngày đi muộn là 0; 1; 2; 3; 4 của các công nhân trong tháng 10. Ta có:

\({f_0} = \frac{{20}}{{40}} \cdot 100\% = 50\% ;\,\,\,{f_1} = \frac{{10}}{{40}} \cdot 100\% = 25\% ;\,\,\,{f_2} = \frac{6}{{40}} \cdot 100\% = 15\% ;\)

\({f_3} = \frac{2}{{40}} \cdot 100\% = 5\% ;\,\,\,{f_4} = \frac{2}{{40}} \cdot 100\% = 5\% ;\)

⦁ Gọi f’₀, f’₁, f’₂, f’₃, f’₄ lần lượt là tần số tương đối của số ngày đi muộn là 0; 1; 2; 3; 4 của các công nhân trong tháng 11. Ta có:

\({f_0}^\prime = \frac{{28}}{{40}} \cdot 100\% = 70\% ;\,\,\,{f_1}^\prime = \frac{8}{{40}} \cdot 100\% = 20\% ;\)

\({f_2}^\prime = \frac{4}{{40}} \cdot 100\% = 10\% ;\,\,\,{f_3}^\prime = {f_4}^\prime = 0\% .\)

b) Để so sánh tình trạng đi làm muộn của các công nhân giữa tháng 10 và tháng 11, ta có thể sử dụng biểu đồ cột kép mô tả tần số tương đối của số ngày đi muộn.

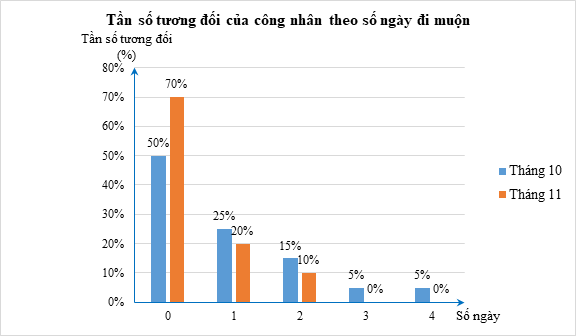
c) So với tháng 10, trong tháng 11, tần số tương đối của công nhân không đi làm muộn ngày nào tăng 20%; tần số tương đối của công nhân đi làm muộn 1 ngày và 2 ngày giảm; không còn công nhân đi muộn nhiều hơn 2 ngày. Vậy ý kiến cho rằng so với tháng 10, tình trạng đi muộn đã được cải thiện trong tháng 11 là hợp lí.

Tổng các tần số tương đối là: 42,5% + 35% + 15% + 7,5% = 100%.

Do đó, nếu có số liệu về tần số tương đối sai thì phải có ít nhất hai số liệu sai.

Mà chỉ có một số liệu sai trong bảng, nên các giá trị tần số tương đối đều chính xác.

Ta có \(\frac{6}{{7,5}} = \frac{{12}}{{15}} = \frac{{28}}{{35}} \ne \frac{{30}}{{42,5}},\) do đó số liệu tần số 30 là sai.

Theo tính chất tỉ lệ thức, ta có giá trị đúng là \(\frac{{28 \cdot 42,5}}{{35}} = 34.\)

Vậy bảng số liệu đúng như sau: