Giải SBT Toán 9 Chân trời sáng tạo Bài 3. Hình cầu có đáp án

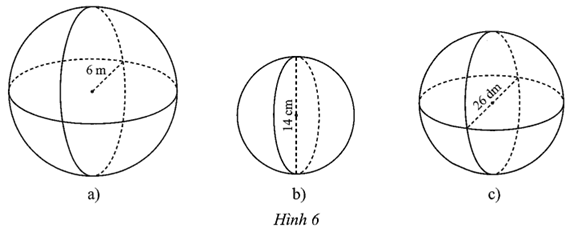
⦁ Hình 6a:

Diện tích của mặt cầu là:

S = 4πR² = 4.π.6² = 144π (m²).

Thể tích của hình cầu là:

\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3} \cdot \pi \cdot {6^3} = 288\pi \) (m³).

⦁ Hình 6b:

Bán kính của hình cầu là: 14 : 2 = 7 (dm).

Diện tích của mặt cầu là:

   S = 4πR² = 4.π.7² = 196π (cm²).

Thể tích của hình cầu là:

   \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3} \cdot \pi \cdot {7^3} = \frac{{1\,\,372\pi }}{3}\) (cm³).

⦁ Hình 6c:

Bán kính của hình cầu là: 26 : 2 = 13 (dm).

Diện tích của mặt cầu là:

   S = 4πR² = 4.π.13² = 676π (dm²).

Thể tích của hình cầu là:

   \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3} \cdot \pi \cdot {13^3} = \frac{{8\,\,788\pi }}{3}\) (dm³).

Khi cắt hình cầu bởi một mặt phẳng thì phần chung của mặt cầu và mặt phẳng là một hình tròn.

Do đó, đường viền của mặt nước và trái bóng có dạng đường tròn.

a) Ta có: \(V = \frac{4}{3}\pi {R^3},\) suy ra \(R = \sqrt[3]{{\frac{{3V}}{{4\pi }}}} = \sqrt[3]{{\frac{{3 \cdot 450}}{{4\pi }}}} = \sqrt[3]{{\frac{{675}}{{2\pi }}}}\) (m);

Khi đó, \(S = 4\pi {R^2} = 4 \cdot \pi \cdot {\left( {\sqrt[3]{{\frac{{675}}{{2\pi }}}}} \right)^2} \approx 284\) (m²).

b) Ta có: \(V = \frac{4}{3}\pi {R^3},\) suy ra \(R = \sqrt[3]{{\frac{{3V}}{{4\pi }}}} = \sqrt[3]{{\frac{{3 \cdot 250}}{{4\pi }}}} = \sqrt[3]{{\frac{{375}}{{2\pi }}}}\) (dm);

Khi đó, \(S = 4\pi {R^2} = 4 \cdot \pi \cdot {\left( {\sqrt[3]{{\frac{{375}}{{2\pi }}}}} \right)^2} \approx 192\) (dm²).

c) Ta có: \(V = \frac{4}{3}\pi {R^3},\) suy ra \[R = \sqrt[3]{{\frac{{3V}}{{4\pi }}}} = \sqrt[3]{{\frac{{3 \cdot 62}}{{4\pi }}}} = \sqrt[3]{{\frac{{93}}{{2\pi }}}}\] (cm);

Khi đó, \(S = 4\pi {R^2} = 4 \cdot \pi \cdot {\left( {\sqrt[3]{{\frac{{93}}{{2\pi }}}}} \right)^2} \approx 76\) (cm²).

a) Ta có: S = 4πR², suy ra \(R = \sqrt {\frac{S}{{4\pi }}} = \sqrt {\frac{{170}}{{4\pi }}} \) (m).

Khi đó, \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {\left( {\sqrt {\frac{{170}}{{4\pi }}} } \right)^3} \approx 208\) (m³).

b) Ta có: S = 4πR², suy ra \(R = \sqrt {\frac{S}{{4\pi }}} = \sqrt {\frac{{190}}{{4\pi }}} \) (dm).

Khi đó, \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {\left( {\sqrt {\frac{{190}}{{4\pi }}} } \right)^3} \approx 246\) (dm³).

c) Ta có: S = 4πR², suy ra \(R = \sqrt {\frac{S}{{4\pi }}} = \sqrt {\frac{{1\,\,973}}{{4\pi }}} \) (cm).

Khi đó, \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {\left( {\sqrt {\frac{{1\,\,973}}{{4\pi }}} } \right)^3} \approx 8\,\,241\) (cm³).

Thể tích của viên bi đặc đó là: \(\frac{4}{3} \cdot \pi \cdot 0,{8^3} = \frac{{256\pi }}{{375}}\) (cm³).

Khối lượng của một viên bi là:

   \(\frac{{256\pi }}{{375}} \cdot 7,85 = \frac{{10\,\,048\pi }}{{1\,\,875}}\) (g).

Ta có: 2 kg = 2 000 (g) và \(2\,\,000:\frac{{10\,\,048\pi }}{{1\,\,875}} \approx 118,796.\)

Vậy với 2 kg thép thì chế tạo được 118 viên bi.