Câu hỏi:
28/08/2024 288
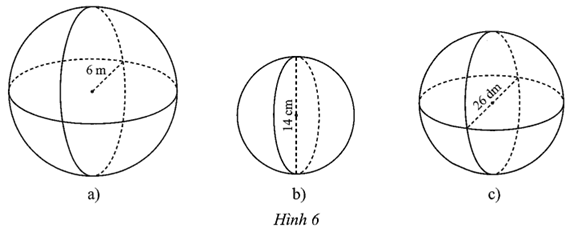
Tính thể tích của hình cầu có diện tích mặt cầu là:
a) 170 m2;
b) 190 dm2;
c) 1 973 cm2.
(Làm tròn kết quả đến hàng đơn vị của mét khối, đềximét khối, xăngtimét khối.)
Tính thể tích của hình cầu có diện tích mặt cầu là:
a) 170 m2;
b) 190 dm2;
c) 1 973 cm2.
(Làm tròn kết quả đến hàng đơn vị của mét khối, đềximét khối, xăngtimét khối.)
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Ta có: S = 4πR2, suy ra \(R = \sqrt {\frac{S}{{4\pi }}} = \sqrt {\frac{{170}}{{4\pi }}} \) (m).
Khi đó, \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {\left( {\sqrt {\frac{{170}}{{4\pi }}} } \right)^3} \approx 208\) (m3).
b) Ta có: S = 4πR2, suy ra \(R = \sqrt {\frac{S}{{4\pi }}} = \sqrt {\frac{{190}}{{4\pi }}} \) (dm).
Khi đó, \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {\left( {\sqrt {\frac{{190}}{{4\pi }}} } \right)^3} \approx 246\) (dm3).
c) Ta có: S = 4πR2, suy ra \(R = \sqrt {\frac{S}{{4\pi }}} = \sqrt {\frac{{1\,\,973}}{{4\pi }}} \) (cm).
Khi đó, \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {\left( {\sqrt {\frac{{1\,\,973}}{{4\pi }}} } \right)^3} \approx 8\,\,241\) (cm3).
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
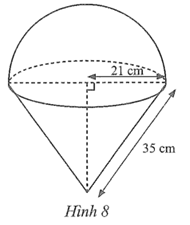
Chiều cao của hình nón là:
\(h = \sqrt {{l^2} - {r^2}} = \sqrt {{{35}^2} - {{21}^2}} = \sqrt {784} = 28\) (cm).
⦁ Thể tích của hình nón là:
\({V_1} = \frac{1}{3} \cdot \pi \cdot {21^2} \cdot 28 = 4\,\,116\pi \) (cm3).
Thể tích của nửa hình cầu là:
\({V_2} = \frac{1}{2} \cdot \left( {\frac{4}{3} \cdot \pi \cdot {{21}^3}} \right) = 6\,\,174\pi \) (cm3).
Thể tích của vật thể là:
V = V1 + V2 = 4 116π + 6 174π = 10 290π ≈ 32 327 (cm3).
⦁ Diện tích xung quanh của hình nón là:
S1 = π.21.35 = 735π (cm2).
Diện tích bề mặt của nửa hình cầu là:
\({S_2} = \frac{1}{2} \cdot \left( {4\pi \cdot {{21}^2}} \right) = 882\pi \) (cm2).
Diện tích bề mặt của vật thể là:
S = S1 + S2 = 735π + 882π = 1 617π ≈ 5 080 (cm2).
Lời giải
Thể tích của viên bi đặc đó là: \(\frac{4}{3} \cdot \pi \cdot 0,{8^3} = \frac{{256\pi }}{{375}}\) (cm3).
Khối lượng của một viên bi là:
\(\frac{{256\pi }}{{375}} \cdot 7,85 = \frac{{10\,\,048\pi }}{{1\,\,875}}\) (g).
Ta có: 2 kg = 2 000 (g) và \(2\,\,000:\frac{{10\,\,048\pi }}{{1\,\,875}} \approx 118,796.\)
Vậy với 2 kg thép thì chế tạo được 118 viên bi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất)- Đề số 1