Cho biết 1 cm3 thép có khối lượng là 7,85 g. Với 2 kg thép thì chế tạo được bao nhiêu viên bi đặc dạng hình cầu có bán kính 0,8 cm (bỏ qua hao hụt trong quá trình chế tạo)?
Cho biết 1 cm3 thép có khối lượng là 7,85 g. Với 2 kg thép thì chế tạo được bao nhiêu viên bi đặc dạng hình cầu có bán kính 0,8 cm (bỏ qua hao hụt trong quá trình chế tạo)?
Câu hỏi trong đề: Giải SBT Toán 9 Chân trời sáng tạo Bài 3. Hình cầu có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Thể tích của viên bi đặc đó là: \(\frac{4}{3} \cdot \pi \cdot 0,{8^3} = \frac{{256\pi }}{{375}}\) (cm3).
Khối lượng của một viên bi là:
\(\frac{{256\pi }}{{375}} \cdot 7,85 = \frac{{10\,\,048\pi }}{{1\,\,875}}\) (g).
Ta có: 2 kg = 2 000 (g) và \(2\,\,000:\frac{{10\,\,048\pi }}{{1\,\,875}} \approx 118,796.\)
Vậy với 2 kg thép thì chế tạo được 118 viên bi.
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
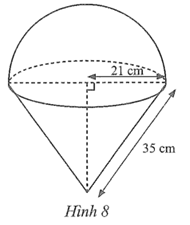
Chiều cao của hình nón là:
\(h = \sqrt {{l^2} - {r^2}} = \sqrt {{{35}^2} - {{21}^2}} = \sqrt {784} = 28\) (cm).
⦁ Thể tích của hình nón là:
\({V_1} = \frac{1}{3} \cdot \pi \cdot {21^2} \cdot 28 = 4\,\,116\pi \) (cm3).
Thể tích của nửa hình cầu là:
\({V_2} = \frac{1}{2} \cdot \left( {\frac{4}{3} \cdot \pi \cdot {{21}^3}} \right) = 6\,\,174\pi \) (cm3).
Thể tích của vật thể là:
V = V1 + V2 = 4 116π + 6 174π = 10 290π ≈ 32 327 (cm3).
⦁ Diện tích xung quanh của hình nón là:
S1 = π.21.35 = 735π (cm2).
Diện tích bề mặt của nửa hình cầu là:
\({S_2} = \frac{1}{2} \cdot \left( {4\pi \cdot {{21}^2}} \right) = 882\pi \) (cm2).
Diện tích bề mặt của vật thể là:
S = S1 + S2 = 735π + 882π = 1 617π ≈ 5 080 (cm2).
Lời giải
a) Ta có: \(V = \frac{4}{3}\pi {R^3},\) suy ra \(R = \sqrt[3]{{\frac{{3V}}{{4\pi }}}} = \sqrt[3]{{\frac{{3 \cdot 450}}{{4\pi }}}} = \sqrt[3]{{\frac{{675}}{{2\pi }}}}\) (m);
Khi đó, \(S = 4\pi {R^2} = 4 \cdot \pi \cdot {\left( {\sqrt[3]{{\frac{{675}}{{2\pi }}}}} \right)^2} \approx 284\) (m2).
b) Ta có: \(V = \frac{4}{3}\pi {R^3},\) suy ra \(R = \sqrt[3]{{\frac{{3V}}{{4\pi }}}} = \sqrt[3]{{\frac{{3 \cdot 250}}{{4\pi }}}} = \sqrt[3]{{\frac{{375}}{{2\pi }}}}\) (dm);
Khi đó, \(S = 4\pi {R^2} = 4 \cdot \pi \cdot {\left( {\sqrt[3]{{\frac{{375}}{{2\pi }}}}} \right)^2} \approx 192\) (dm2).
c) Ta có: \(V = \frac{4}{3}\pi {R^3},\) suy ra \[R = \sqrt[3]{{\frac{{3V}}{{4\pi }}}} = \sqrt[3]{{\frac{{3 \cdot 62}}{{4\pi }}}} = \sqrt[3]{{\frac{{93}}{{2\pi }}}}\] (cm);
Khi đó, \(S = 4\pi {R^2} = 4 \cdot \pi \cdot {\left( {\sqrt[3]{{\frac{{93}}{{2\pi }}}}} \right)^2} \approx 76\) (cm2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập