Giải SBT Toán 9 Chân trời sáng tạo Bài 2. Hình nón quay có đáp án
28 người thi tuần này 4.6 213 lượt thi 5 câu hỏi
🔥 Đề thi HOT:
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
32.9 K lượt thi
3 câu hỏi
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
29.1 K lượt thi
4 câu hỏi
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
7.1 K lượt thi
5 câu hỏi
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
2 K lượt thi
12 câu hỏi
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
6.2 K lượt thi
87 câu hỏi
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
2 K lượt thi
12 câu hỏi
Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất)- Đề số 1
7.5 K lượt thi
5 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
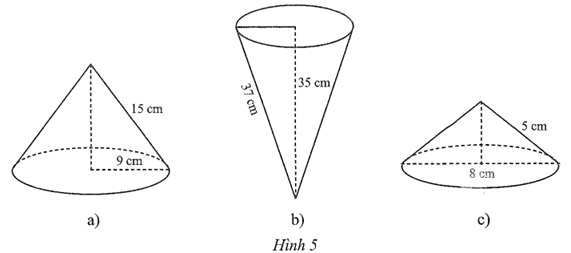
⦁ Hình 5a:
Chiều cao của hình nón là:
\(h = \sqrt {{l^2} - {r^2}} = \sqrt {{{15}^2} - {9^2}} = \sqrt {144} = 12\) (cm).
Bán kính đáy, chiều cao, độ dài đường sinh của hình nón lần lượt là r = 9 cm, h = 12 cm, l = 15 cm.
⦁ Hình 5b:
Bán kính đáy của hình nón là:
\(r = \sqrt {{l^2} - {h^2}} = \sqrt {{{37}^2} - {{35}^2}} = \sqrt {144} = 12\) (cm).
Bán kính đáy, chiều cao, độ dài đường sinh của hình nón lần lượt là r = 12 cm, h = 35 cm, l = 37 cm.
⦁ Hình 5c:
Bán kính đáy của hình nón là: r = 8 : 2 = 4 (cm).
Chiều cao của hình nón là:
\(h = \sqrt {{l^2} - {r^2}} = \sqrt {{5^2} - {4^2}} = \sqrt 9 = 3\) (cm).
Bán kính đáy, chiều cao, độ dài đường sinh của hình nón lần lượt là r = 4 cm, h = 3 cm, l = 5 cm.
Lời giải
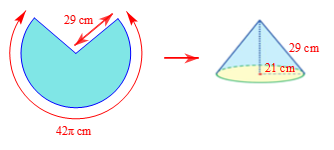
Gọi r là bán kính đáy của hình nón, độ dài cung của hình quạt tròn bằng chu vi đáy của hình nón, khi đó: 2πr = 42π, suy ra r = 21 cm.
Độ dài đường sinh l của hình nón bằng bán kính của hình quạt tròn, suy ra l = 29 cm.
Chiều cao của hình nón là:
\(h = \sqrt {{l^2} - {r^2}} = \sqrt {{{29}^2} - {{21}^2}} = \sqrt {400} = 20\) (cm).
Vậy bán kính đáy và chiều cao của hình nón lần lượt là r = 21 cm và h = 20 cm.
Lời giải
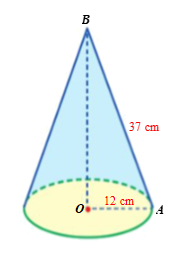
Hình tạo thành là một hình nón có bán kính đáy r = OA = 12 cm và đường sinh l = AB = 37 cm, suy ra chiều cao của hình nón là:
\(OB = h = \sqrt {{l^2} - {r^2}} = \sqrt {{{37}^2} - {{12}^2}} = \sqrt {1\,\,225} = 35\) (cm).
Diện tích xung quanh của hình nón là:
S = πrl = π.12.37 = 444π (cm2).
Thể tích của hình nón là:
\(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3} \cdot \pi \cdot {12^2} \cdot 35 = 1\,\,680\pi \) (cm3).
Lời giải
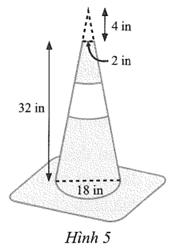
a) Bán kính đáy của hình nón bị cắt đi là: r1 = 2 : 2 = 1 (in).
Độ dài đường sinh của hình nón bị cắt đi là:
\({l_1} = \sqrt {h_1^2 + r_1^2} = \sqrt {{4^2} + {1^2}} = \sqrt {17} \) (in).
Diện tích xung quanh của hình nón bị cắt đi là:
\({S_1} = \pi {r_1}{l_1} = \pi \cdot 1 \cdot \sqrt {17} = \pi \sqrt {17} \) (in2).
Bán kính đáy của hình nón khi chưa bị cắt đi là: r2 = 18 : 2 = 9 (in).
Độ dài đường sinh của hình nón khi chưa bị cắt là:
\({l_2} = \sqrt {h_2^2 + r_2^2} = \sqrt {{{\left( {32 + 4} \right)}^2} + {9^2}} = \sqrt {1\,\,377} = 9\sqrt {17} \) (in).
Diện tích xung quanh của hình nón chưa bị cắt đi là:
\({S_2} = \pi {r_2}{l_2} = \pi \cdot 9 \cdot 9\sqrt {17} = 81\pi \sqrt {17} \) (in2).
Diện tích xung quanh của cọc tiêu là:
\[{S_2} - {S_1} = 81\pi \sqrt {17} - \pi \sqrt {17} = 80\pi \sqrt {17} \approx 1\,\,036\] (in2).
b) Thể tích hình nón bị cắt đi là:
\({V_1} = \frac{1}{3}\pi r_1^2{h_1} = \frac{1}{3} \cdot \pi \cdot {1^1} \cdot 4 = \frac{4}{3}\pi \) (in3).
Thể tích của hình nón khi chưa bị cắt là:
\({V_2} = \frac{1}{3}\pi r_2^2{h_2} = \frac{1}{3}\pi \cdot {9^2} \cdot \left( {32 + 4} \right) = 972\pi \) (in3).
Thể tích của cọc tiêu là:
V2 – V1 = 972π – \(\frac{4}{3}\)π = \(\frac{{2\,\,912}}{3}\)π ≈ 3 049 (in3).
Lời giải
Chiếc nón lá có dạng hình nón với vành lớn nhất chính là đường tròn đáy của hình nón, vì vậy bán kính đáy là r = 40 : 2 = 20 cm. Khoảng cách từ đỉnh cao nhất của chiếc nón đến một điểm trên vành lớn nhất chính là độ dài đường sinh, vì vậy l = 32 cm.
Diện tích xung quanh của chiếc nón lá là:
S = πrl = π . 20 . 32 = 640π ≈ 2 011 (cm2).