Giải SBT Toán 9 Chân trời sáng tạo Bài 4. Hình quạt tròn và hình vành khuyên có đáp án
36 người thi tuần này 4.6 417 lượt thi 8 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
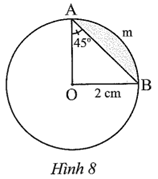
a) Xét ∆OAB cân tại O (do OA = OB) nên \(\widehat {AOB} = 180^\circ - 2\widehat {OAB} = 180^\circ - 2 \cdot 45^\circ = 90^\circ .\)
Suy ra
b) Độ dài cung AmB là:
c) Diện tích hình quạt tròn OAmB là:
\({S_{OAmB}} = \frac{{\pi \cdot {2^2} \cdot 90}}{{360}} = \pi \approx 3,14\,\,({\rm{c}}{{\rm{m}}^2}).\)
d) Do ∆OAB có \(\widehat {AOB} = 90^\circ \) nên ∆OAB vuông tại O.
Diện tích tam giác OAB là:
\({S_{\Delta OAB}} = \frac{1}{2} \cdot OA \cdot OB = \frac{1}{2} \cdot 2 \cdot 2 = 2\,\,{\rm{(c}}{{\rm{m}}^2}).\)
Diện tích hình viên phân giới hạn bởi cung AmB và dây AB bằng:
SOAmB – S∆OAB = π – 2 ≈ 3,14 – 2 = 1,14 (cm2).
Lời giải
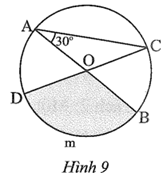
a) Xét ∆OAC cân tại O (do OA = OC), suy ra \[\widehat {OCA} = \widehat {OAC} = 30^\circ .\]
Lại có \[\widehat {OCA} + \widehat {OAC} + \widehat {AOC} = 180^\circ \]
Suy ra \[\widehat {AOC} = 180^\circ - \widehat {OCA} - \widehat {OAC} = 180^\circ - 30^\circ - 30^\circ = 120^\circ \]
Do đó \[\widehat {DOB} = \widehat {AOC} = 120^\circ \] (đối đỉnh).
Do AB = 3 cm, suy ra \[AO = OB = \frac{1}{2}AB = \frac{1}{2} \cdot 3 = 1,5\] (cm).
Cung BmD có số đo 120°, bán kính R = 1,5 cm có độ dài là:
b) Diện tích hình quạt tròn OBmD bán kính R = 1,5 cm là:
\({S_{OBmD}} = \frac{{\pi \cdot 1,{5^2} \cdot 120}}{{360}} = \frac{3}{4}\pi \approx 2,36\,\,({\rm{c}}{{\rm{m}}^2}).\)
Lời giải
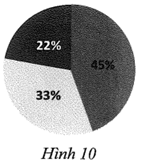
Diện tích hình quạt tròn ứng với số liệu 45% là:
\(45\% \cdot \pi {R^2} = 45\% \cdot \pi \cdot {15^2} = \frac{{405\pi }}{4} \approx 318,09\,\,(\;{\rm{c}}{{\rm{m}}^2}).\)
Diện tích hình quạt tròn ứng với số liệu 33 % là:
\(33\% \cdot \pi {R^2} = 33\% \cdot \pi \cdot {15^2} = \frac{{297\pi }}{4} \approx 233,26\,\,(\;{\rm{c}}{{\rm{m}}^2}).\)
Diện tích hình quạt tròn ứng với số liệu 22 % là:
\[22\% \cdot \pi \cdot {R^2} = 22\% \cdot \pi \cdot {15^2} = \frac{{99\pi }}{2} \approx 155,51\,\,(\;{\rm{c}}{{\rm{m}}^2}).\]
Lời giải
Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 8 cm) và (O; 24 cm) là:
S = π(R2 – r2) = π(242 – 82) = 512π ≈ 1 608,50 (cm2).
Lời giải
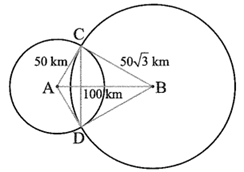
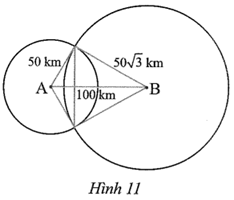
Gọi C và D là giao điểm của hai đường tròn (A; 50 km) và \(\left( {B;\,\,50\sqrt 3 \;\,{\rm{cm}}} \right).\)
Ta có: \[A{C^2} + B{C^2} = {50^2} + {\left( {50\sqrt 3 } \right)^2} = 2\,\,500 + 7\,\,500 = 10\,\,000;\]
AB2 = 1002 = 10 000.
Ta thấy AC2 + BC2 = AB2, suy ra ∆ABC vuông tại C (định lí Pythagore đảo).
Xét ∆ABC vuông tại C có:
\(\sin \widehat {ABC} = \frac{{AC}}{{AB}} = \frac{1}{2},\) suy ra \(\widehat {ABC} = 30^\circ .\)
Suy ra \(\widehat {CAB} = 90^\circ - \widehat {ABC} = 90^\circ - 30^\circ = 60^\circ .\)
Tương tự, ta có: \(\widehat {ABD} = 30^\circ ;\,\,\widehat {BAD} = 60^\circ .\)
Do đó \(\widehat {CBD} = \widehat {ABC} + \widehat {ABD} = 30^\circ + 30^\circ = 60^\circ ;\)
\(\widehat {CAD} = \widehat {BAC} + \widehat {BAD} = 60^\circ + 60^\circ = 120^\circ .\)
Xét ∆BCD có BC = BD và \[\widehat {CBD} = 60^\circ \] nên là tam giác đều, suy ra \(CD = 50\sqrt 3 \;{\rm{km}}.\)
Diện tích của hình quạt tròn ACD được giới hạn bởi bán kính AC, bán kính AD và cung nhỏ CD của đường tròn (A; 50 km) là:
\({S_1} = \frac{{\pi \cdot {{50}^2} \cdot 120}}{{360}} = \frac{{2\,\,500\pi }}{3}\,\,(\;{\rm{k}}{{\rm{m}}^2}).\)
Diện tích hình quạt tròn BCD được giới hạn bởi bán kính BC, bán kính BD và cung nhỏ CD của đường tròn \(\left( {B;\,\,50\sqrt 3 \;{\rm{cm}}} \right)\) là:
\({S_2} = \frac{{\pi \cdot {{\left( {50\sqrt 3 } \right)}^2} \cdot 60}}{{360}} = 1\,\,250\pi \,\,({\rm{k}}{{\rm{m}}^2}).\)
Diện tích tứ giác ABCD là:
\({S_{ABCD}} = \frac{1}{2}AB \cdot CD = \frac{1}{2} \cdot 100 \cdot 50\sqrt 3 = 2\,\,500\sqrt 3 \,\,(\;{\rm{k}}{{\rm{m}}^2}).\)
Diện tích của khu vực có thể đặt thiết bị thu sóng sao cho thu được cả hai sóng phát từ trạm A và trạm B là
\({S_1} + {S_2} - {S_{ABCD}} = \frac{{2\,\,500\pi }}{3} + 1\,\,250\pi - 2\,\,500\sqrt 3 \approx 2\,\,214,86\,\,(\;{\rm{k}}{{\rm{m}}^2}).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.