Quảng cáo
Trả lời:
Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 8 cm) và (O; 24 cm) là:
S = π(R2 – r2) = π(242 – 82) = 512π ≈ 1 608,50 (cm2).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
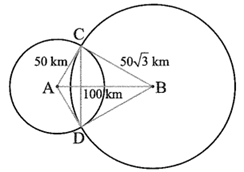
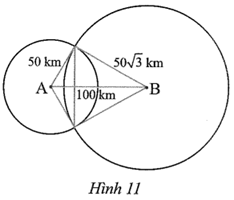
Gọi C và D là giao điểm của hai đường tròn (A; 50 km) và \(\left( {B;\,\,50\sqrt 3 \;\,{\rm{cm}}} \right).\)
Ta có: \[A{C^2} + B{C^2} = {50^2} + {\left( {50\sqrt 3 } \right)^2} = 2\,\,500 + 7\,\,500 = 10\,\,000;\]
AB2 = 1002 = 10 000.
Ta thấy AC2 + BC2 = AB2, suy ra ∆ABC vuông tại C (định lí Pythagore đảo).
Xét ∆ABC vuông tại C có:
\(\sin \widehat {ABC} = \frac{{AC}}{{AB}} = \frac{1}{2},\) suy ra \(\widehat {ABC} = 30^\circ .\)
Suy ra \(\widehat {CAB} = 90^\circ - \widehat {ABC} = 90^\circ - 30^\circ = 60^\circ .\)
Tương tự, ta có: \(\widehat {ABD} = 30^\circ ;\,\,\widehat {BAD} = 60^\circ .\)
Do đó \(\widehat {CBD} = \widehat {ABC} + \widehat {ABD} = 30^\circ + 30^\circ = 60^\circ ;\)
\(\widehat {CAD} = \widehat {BAC} + \widehat {BAD} = 60^\circ + 60^\circ = 120^\circ .\)
Xét ∆BCD có BC = BD và \[\widehat {CBD} = 60^\circ \] nên là tam giác đều, suy ra \(CD = 50\sqrt 3 \;{\rm{km}}.\)
Diện tích của hình quạt tròn ACD được giới hạn bởi bán kính AC, bán kính AD và cung nhỏ CD của đường tròn (A; 50 km) là:
\({S_1} = \frac{{\pi \cdot {{50}^2} \cdot 120}}{{360}} = \frac{{2\,\,500\pi }}{3}\,\,(\;{\rm{k}}{{\rm{m}}^2}).\)
Diện tích hình quạt tròn BCD được giới hạn bởi bán kính BC, bán kính BD và cung nhỏ CD của đường tròn \(\left( {B;\,\,50\sqrt 3 \;{\rm{cm}}} \right)\) là:
\({S_2} = \frac{{\pi \cdot {{\left( {50\sqrt 3 } \right)}^2} \cdot 60}}{{360}} = 1\,\,250\pi \,\,({\rm{k}}{{\rm{m}}^2}).\)
Diện tích tứ giác ABCD là:
\({S_{ABCD}} = \frac{1}{2}AB \cdot CD = \frac{1}{2} \cdot 100 \cdot 50\sqrt 3 = 2\,\,500\sqrt 3 \,\,(\;{\rm{k}}{{\rm{m}}^2}).\)
Diện tích của khu vực có thể đặt thiết bị thu sóng sao cho thu được cả hai sóng phát từ trạm A và trạm B là
\({S_1} + {S_2} - {S_{ABCD}} = \frac{{2\,\,500\pi }}{3} + 1\,\,250\pi - 2\,\,500\sqrt 3 \approx 2\,\,214,86\,\,(\;{\rm{k}}{{\rm{m}}^2}).\)
Lời giải
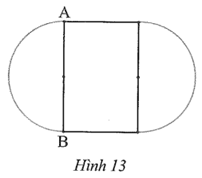
a) Bán kính của chiếc bàn hình tròn ban đầu là: \(\frac{{1,2}}{2} = 0,6{\rm{\;(m)}}{\rm{.}}\)
Diện tích mặt bàn ban đầu là:
\(S = \pi \cdot 0,{6^2} = \frac{{9\pi }}{{25}}\,(\;{{\rm{m}}^2}).\)
Theo bài, diện tích mặt bàn tăng gấp đôi sau khi nới nên diện tích phần mặt bàn hình chữ nhật bằng diện tích mặt bàn ban đầu, và bằng \(\frac{{9\pi }}{{25}}{\rm{\;}}{{\rm{m}}^2}{\rm{.}}\)
Kích thước còn lại của hình chữ nhật là:
\(\frac{{9\pi }}{{25}}:1,2 = \frac{{3\pi }}{{10}} \approx 0,94{\rm{\;(m)}}{\rm{.}}\)
b) Chu vi mặt bàn ban đầu là:
\(C = 2 \cdot \pi \cdot 0,6 = \frac{{6\pi }}{5}{\rm{\;(m)}}{\rm{.}}\)
Theo bài, chu vi mặt bàn tăng gấp đôi sau khi nới và phần chu vi tăng lên chính là hai lần độ dài cạnh còn lại của phần mặt bàn hình chữ nhật và bằng \(\frac{{6\pi }}{5}{\rm{\;m}}.\)
Kích thước còn lại của hình chữ nhật là:
\(\frac{{6\pi }}{5}:2 = \frac{{3\pi }}{5} \approx 1,89{\rm{\;(m)}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.