Giải SBT Toán 9 Chân trời sáng tạo Bài tập cuối chương 5 có đáp án
46 người thi tuần này 4.6 468 lượt thi 18 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
19 bài tập Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: C
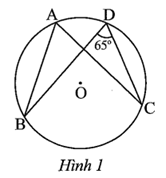
Ta có: \[\widehat {BAC} = \widehat {BDC} = 65^\circ \] (hai góc nội tiếp đường tròn cùng chắn dây cung BC).
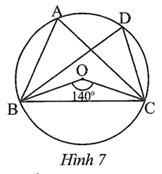
Lời giải
Đáp án đúng là: D
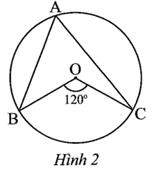
Ta có: \[\widehat {BAC} = \frac{1}{2}\widehat {BOC} = \frac{1}{2} \cdot 120^\circ = 60^\circ \] (góc nội tiếp và góc ở tâm cùng chắn cung BC).
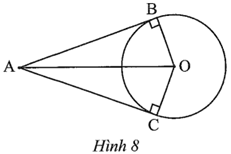
Lời giải
Đáp án đúng là: A
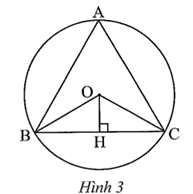
Ta có:
Suy ra nên hay
Xét ∆OBC cân tại O (do OB = OC) nên đường cao OH đồng thời là đường trung tuyến và đường phân giác của tam giác, do đó BC = 2BH và \(\widehat {BOH} = \frac{1}{2}\widehat {BOC} = \frac{1}{2} \cdot 120^\circ = 60^\circ .\)
Xét ∆OBH vuông tại H, ta có:
\(BH = OB \cdot \sin \widehat {BOH} = R \cdot \sin 60^\circ = \frac{{R\sqrt 3 }}{2}.\)
Như vậy, \(BC = 2BH = 2 \cdot \frac{{R\sqrt 3 }}{2} = R\sqrt 3 .\)
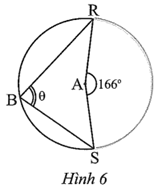
Lời giải
Đáp án đúng là: B
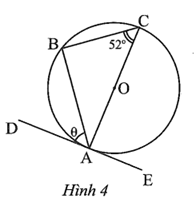
Vì DE là tiếp tuyến của đường tròn (O) nên DE ⊥ OA tại A, suy ra \(\widehat {DAO} = 90^\circ .\)
Do đó \(\widehat {DAB} + \widehat {BAO} = 90^\circ \) hay \(\widehat {DAB} = 90^\circ - \widehat {BAO}.\,\,\left( 1 \right)\)
Xét ∆OAB cân tại O (do OA = OB) có:
\(\widehat {BAO} = \frac{{180^\circ - \widehat {AOB}}}{2} = 90^\circ - \frac{1}{2}\widehat {AOB}.\)
Mà \(\widehat {ACB} = \frac{1}{2}\widehat {AOB}\) (góc nội tiếp và góc ở tâm cùng chắn cung AB của đường tròn (O)).
Do đó \(\widehat {BAO} = 90^\circ - \widehat {ACB}\) hay \(\widehat {ACB} = 90^\circ - \widehat {BAO}.\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra \(\theta = \widehat {DAB} = \widehat {ACB} = 52^\circ .\)
Lời giải
Đáp án đúng là: A
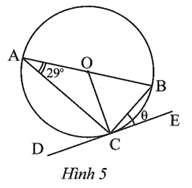
Chứng minh tương tự Câu 4, trang 99, SBT Toán 9 Tập một, ta có:
\(\widehat {BCE} = \widehat {BAC} = 29^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.