Quảng cáo
Trả lời:
Đáp án đúng là: A
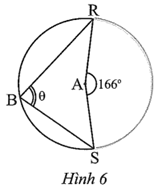
Ta có: \(\widehat {RBS} = \frac{1}{2}\widehat {RAS}\) (góc nội tiếp và góc ở tâm cùng chắn cung RS của đường tròn (A)).
Suy ra \(\theta = \widehat {RBS} = \frac{1}{2}\widehat {RAS} = \frac{1}{2} \cdot 166^\circ = 83^\circ .\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
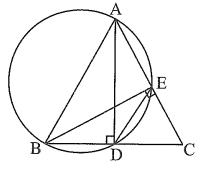
a) Ta có D, E cùng nằm trên đường tròn đường kính AB nên \(\widehat {ADB} = \widehat {AEB} = 90^\circ \) hay AD ⊥ BC và BE ⊥ AC.
Xét ∆ABC cân tại A có AD là đường cao nên đồng thời là đường trung tuyến của tam giác, do đó D là trung điểm BC, suy ra \(DB = DC = \frac{1}{2}BC.\)
Xét ∆BEC vuông tại E có ED là đường trung tuyến ứng với cạnh huyền BC nên \(ED = \frac{1}{2}BC.\)
Do đó DE = DB = DC.
Vậy ∆BDE cân tại D.
b) Xét ∆ABC cân tại A có AD là đường cao nên đồng thời là tia phân giác của \(\widehat {BAC},\) do đó \(\widehat {BAD} = \frac{1}{2}\widehat {BAC}.\)
Ta có \(\widehat {DBE} = \widehat {DEB}\) (do ∆BDE cân tại D) và \(\widehat {BAD} = \widehat {BED}\) (hai góc nội tiếp cùng chắn cung BD).
Suy ra \[\widehat {DBE} = \frac{1}{2}\widehat {BAC}\] hay \[\widehat {CBE} = \frac{1}{2}\widehat {BAC}.\]
Lời giải
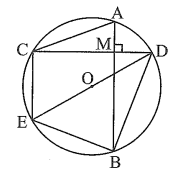
Do AB ⊥ CD nên \(\widehat {AMC} = \widehat {DMB} = 90^\circ .\)
a) Xét đường tròn (O) có \(\widehat {ACD} = \widehat {ABD}\) (hai góc nội tiếp cùng chắn cung AD).
Xét ∆MAC và ∆MDB, có:
\(\widehat {AMC} = \widehat {DMB} = 90^\circ ,\,\,\widehat {ACM} = \widehat {DBM}\)
Do đó ∆MAC ᔕ ∆MDB (g.g).
Suy ra \(\frac{{MA}}{{MD}} = \frac{{MC}}{{MB}}\) hay MA.MB = MC.MD.
b) Vì DE là đường kính của đường tròn (O) nên \(\widehat {ECD} = \widehat {EBD} = 90^\circ .\)
Suy ra CE ⊥ CD.
Mà AB ⊥ CD nên AB // CE, do đó tứ giác ABEC là hình thang.
Mặt khác, \(\widehat {CAB} + \widehat {ACM} = 90^\circ \) (tổng hai góc nhọn trong ∆ACM vuông tại M);
\(\widehat {EBA} + \widehat {MBD} = \widehat {EBD} = 90^\circ ;\)
\(\widehat {ACM} = \widehat {DBM}\)
Suy ra \(\widehat {EBA} = \widehat {CAB}.\)
Hình thang ABEC có \(\widehat {EBA} = \widehat {CAB}\) nên ABEC là hình thang cân.
c) Xét ∆ACM vuông tại M, theo định lí Pythagore, ta có:
AC2 = MA2 + MC2.
Xét ∆BDM vuông tại M, theo định lí Pythagore, ta có:
BD2 = MB2 + MD2.
Do đó MA2 + MB2 + MC2 + MD2 = AC2 + BD2.
Lại có AC = BE (vì ABEC là hình thang cân) nên:
MA2 + MB2 + MC2 + MD2 = AC2 + BD2 = BE2 + BD2.
Xét ∆BDE vuông tại B, theo định lí Pythagore, ta có:
DE2 = BD2 + BE2.
Do đó MA2 + MB2 + MC2 + MD2 = BE2 + BD2 = DE2 = (2R)2 = 4R2, đây là giá trị không đổi do R không đổi.ở
Vậy tổng MA2 + MB2 + MC2 + MD2 có giá trị không đổi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.