Câu hỏi:
28/08/2024 638
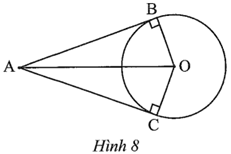
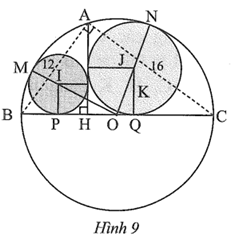
Trong Hình 9, cho biết AB = 12, AC = 16; đường tròn (I) tiếp xúc với AH, BC và đường tròn (O); đường tròn (J) tiếp xúc với AH, BC và đường tròn (O).
Tính:
a) BC, BH.
b) Bán kính R, R’ của đường tròn (I) và (J).
c) Khoảng cách PQ.
Trong Hình 9, cho biết AB = 12, AC = 16; đường tròn (I) tiếp xúc với AH, BC và đường tròn (O); đường tròn (J) tiếp xúc với AH, BC và đường tròn (O).
Tính:
a) BC, BH.
b) Bán kính R, R’ của đường tròn (I) và (J).
c) Khoảng cách PQ.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Áp dụng định lí Pythagore cho tam giác ABC vuông tại A, ta có:
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{{12}^2} + {{16}^2}} = \sqrt {400} = 20.\)
Xét ∆BHA và ∆BAC có:
\[\widehat B\] là góc chung; \[\widehat {BHA} = \widehat {BAC} = 90^\circ .\]
Do đó ∆BHA ᔕ ∆BAC (g.g), suy ra \[\frac{{BA}}{{BC}} = \frac{{BH}}{{BA}}\]
Nên \(BH = \frac{{B{A^2}}}{{BC}} = \frac{{{{12}^2}}}{{20}} = \frac{{144}}{{20}} = 7,2.\)
b) Ta có \[OB = OC = \frac{1}{2}BC = \frac{1}{2} \cdot 20 = 10;\]
OH = OB – BH = 10 – 7,2 = 2,8.
Gọi D là tiếp điểm của đường tròn (I) với AH.
Theo bài, đường tròn (I) tiếp xúc với AH, BC nên ID ⊥ AH và IP ⊥ BC.
Tứ giác IPHD có \(\widehat {IPH} = \widehat {IDH} = \widehat {PHD} = 90^\circ \) và ID = IP nên IPHD là hình vuông.
Do đó PH = IP = R.
Chứng minh tương tự, ta cũng có HQ = IQ = R’.
Áp dụng định lí Pythagore cho tam giác IPO vuông tại P, ta có:
IO2 = IP2 + PO2
Suy ra (OM – IM)2 = IP2 + (OH + PH)2
(10 – R)2 = R2 + (R + 2,8)2
100 – 20R + R2 = R2 + R2 + 5,6R + 7,84
R2 + 25,6R – 92,16 = 0
Phương trình trên có ∆ = 25,62 – 4.1.(–92,16) = 1 024 > 0 và \(\sqrt \Delta = \sqrt {1\,\,024} = 32.\)
Do đó phương trình trên có hai nghiệm là:
\(R = \frac{{ - 25,6 + 32}}{2} = 3,2\) (thỏa mãn);
\(R = \frac{{ - 25,6 - 32}}{2} = - 28,8\) (không thỏa mãn).
Áp dụng định lí Pythagore cho tam giác JQO vuông tại Q, ta có:
JO2 = JQ2 + QO2
Suy ra (ON – JN)2 = R2 + (HQ – OH)2
(10 – R’)2 = R’2 + (R’ – 2,8)2
100 – 20R’ + R’2 = R’2 + R’2 – 5,6R’ + 7,84
R’2 + 14,4R – 92,16 = 0.
Phương trình trên có ∆ = 14,42 – 4.1.(–92,16) = 576 > 0 và \(\sqrt \Delta = \sqrt {576} = 24.\)
Do đó phương trình trên có hai nghiệm là:
\(R = \frac{{ - 14,4 + 24}}{2} = 4,8\) (thỏa mãn);
\(R = \frac{{ - 14,4 - 24}}{2} = - 19,2\) (không thỏa mãn).
c) Ta có PQ = PH + QH = R + R’ = 3,2 + 4,8 = 8.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
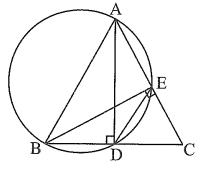
a) Ta có D, E cùng nằm trên đường tròn đường kính AB nên \(\widehat {ADB} = \widehat {AEB} = 90^\circ \) hay AD ⊥ BC và BE ⊥ AC.
Xét ∆ABC cân tại A có AD là đường cao nên đồng thời là đường trung tuyến của tam giác, do đó D là trung điểm BC, suy ra \(DB = DC = \frac{1}{2}BC.\)
Xét ∆BEC vuông tại E có ED là đường trung tuyến ứng với cạnh huyền BC nên \(ED = \frac{1}{2}BC.\)
Do đó DE = DB = DC.
Vậy ∆BDE cân tại D.
b) Xét ∆ABC cân tại A có AD là đường cao nên đồng thời là tia phân giác của \(\widehat {BAC},\) do đó \(\widehat {BAD} = \frac{1}{2}\widehat {BAC}.\)
Ta có \(\widehat {DBE} = \widehat {DEB}\) (do ∆BDE cân tại D) và \(\widehat {BAD} = \widehat {BED}\) (hai góc nội tiếp cùng chắn cung BD).
Suy ra \[\widehat {DBE} = \frac{1}{2}\widehat {BAC}\] hay \[\widehat {CBE} = \frac{1}{2}\widehat {BAC}.\]
Lời giải
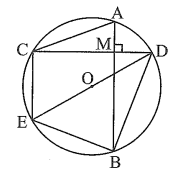
Do AB ⊥ CD nên \(\widehat {AMC} = \widehat {DMB} = 90^\circ .\)
a) Xét đường tròn (O) có \(\widehat {ACD} = \widehat {ABD}\) (hai góc nội tiếp cùng chắn cung AD).
Xét ∆MAC và ∆MDB, có:
\(\widehat {AMC} = \widehat {DMB} = 90^\circ ,\,\,\widehat {ACM} = \widehat {DBM}\)
Do đó ∆MAC ᔕ ∆MDB (g.g).
Suy ra \(\frac{{MA}}{{MD}} = \frac{{MC}}{{MB}}\) hay MA.MB = MC.MD.
b) Vì DE là đường kính của đường tròn (O) nên \(\widehat {ECD} = \widehat {EBD} = 90^\circ .\)
Suy ra CE ⊥ CD.
Mà AB ⊥ CD nên AB // CE, do đó tứ giác ABEC là hình thang.
Mặt khác, \(\widehat {CAB} + \widehat {ACM} = 90^\circ \) (tổng hai góc nhọn trong ∆ACM vuông tại M);
\(\widehat {EBA} + \widehat {MBD} = \widehat {EBD} = 90^\circ ;\)
\(\widehat {ACM} = \widehat {DBM}\)
Suy ra \(\widehat {EBA} = \widehat {CAB}.\)
Hình thang ABEC có \(\widehat {EBA} = \widehat {CAB}\) nên ABEC là hình thang cân.
c) Xét ∆ACM vuông tại M, theo định lí Pythagore, ta có:
AC2 = MA2 + MC2.
Xét ∆BDM vuông tại M, theo định lí Pythagore, ta có:
BD2 = MB2 + MD2.
Do đó MA2 + MB2 + MC2 + MD2 = AC2 + BD2.
Lại có AC = BE (vì ABEC là hình thang cân) nên:
MA2 + MB2 + MC2 + MD2 = AC2 + BD2 = BE2 + BD2.
Xét ∆BDE vuông tại B, theo định lí Pythagore, ta có:
DE2 = BD2 + BE2.
Do đó MA2 + MB2 + MC2 + MD2 = BE2 + BD2 = DE2 = (2R)2 = 4R2, đây là giá trị không đổi do R không đổi.ở
Vậy tổng MA2 + MB2 + MC2 + MD2 có giá trị không đổi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất)- Đề số 1