Bộ 5 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo (Tự luận) có đáp án - Đề 4
21 người thi tuần này 4.6 1 K lượt thi 15 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi Giữa kì 2 Toán 9 trường THCS Lê Quí Đôn (Hồ Chí Minh) năm học 2024-2025 có đáp án
85 lượt thi
6 câu hỏi
Đề thi Giữa kì 2 Toán 9 trường THCS An Nhơn (Hồ Chí Minh) năm học 2024-2025 có đáp án
83 lượt thi
5 câu hỏi
Đề cương ôn tập giữa kì 2 Toán 9 Kết nối tri thức có đáp án - Trắc nghiệm
18 lượt thi
30 câu hỏi
Đề thi Giữa kì 2 Toán 9 trường THCS Ba Đình (Hà Nội) năm học 2024-2025 có đáp án
1 K lượt thi
7 câu hỏi
Đề thi Giữa kì 2 Toán 9 trường THCS Mai Dịch (Hà Nội) năm học 2024-2025 có đáp án
1 K lượt thi
8 câu hỏi
Danh sách câu hỏi:
Đoạn văn 1
(2,0 điểm) Cho hai biểu thức: và .
Lời giải
a) – Xét biểu thức \(A = \frac{{\sqrt x \left( {x + 1} \right)}}{{2\left( {\sqrt x - 1} \right)}}\).
Điều kiện xác định của biểu thức \(A\) và \(x \ge 0\) và \(\sqrt x - 1 \ne 0\) hay \(x \ge 0,\,\,x \ne 1.\)
– Xét biểu thức \(B = \frac{1}{{x + \sqrt x }} + \frac{{2\sqrt x }}{{x - 1}} - \frac{1}{{x - \sqrt x }}\).
Với \(x \ge 0\), ta có:
⦁ \(x + \sqrt x = \sqrt x \left( {\sqrt x + 1} \right)\); \(x - \sqrt x = \sqrt x \left( {\sqrt x - 1} \right);\) \(x - 1 = \left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right).\)
⦁ \(x \ge 0\) nên \(\sqrt x \ge 0,\) suy ra \(\sqrt x + 1 > 0.\)
Điều kiện xác định của biểu thức \(B\) là \(x \ge 0\) và \(\sqrt x \ne 0,\,\,x - 1 \ne 0\) hay \(x > 0,\,\,x \ne 1.\)
Vậy, điều kiện xác định của biểu thức \(A = \frac{{\sqrt x \left( {x + 1} \right)}}{{2\left( {\sqrt x - 1} \right)}}\) là \(x \ge 0,x \ne 1\) và điều kiện xác định của biểu thức \(B = \frac{1}{{x + \sqrt x }} + \frac{{2\sqrt x }}{{x - 1}} - \frac{1}{{x - \sqrt x }}\) là \(x > 0,x \ne 1.\)
Lời giải
b) Thay \(x = \frac{1}{9}\) (thỏa mãn điều kiện) vào biểu thức \(A,\) ta được:
\(A = \frac{{\sqrt {\frac{1}{9}} \left( {\frac{1}{9} + 1} \right)}}{{2\left( {\sqrt {\frac{1}{9}} - 1} \right)}} = \frac{{\frac{1}{3}.\frac{{10}}{9}}}{{2\left( {\frac{1}{3} - 1} \right)}} = \frac{{\frac{{10}}{{27}}}}{{ - \frac{4}{3}}} = - \frac{5}{{18}}.\)
Vậy \(A = - \frac{5}{{18}}\) khi \(x = \frac{1}{9}\).
Lời giải
c) Với \(x > 0,x \ne 1\), ta có:
\(B = \frac{1}{{x + \sqrt x }} + \frac{{2\sqrt x }}{{x - 1}} - \frac{1}{{x - \sqrt x }}\)
\( = \frac{1}{{\sqrt x \left( {\sqrt x + 1} \right)}} + \frac{{2\sqrt x }}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} - \frac{1}{{\sqrt x \left( {\sqrt x - 1} \right)}}\)
\[ = \frac{{\sqrt x - 1}}{{\sqrt x \left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} + \frac{{2\sqrt x \cdot \sqrt x }}{{\sqrt x \left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} - \frac{{\sqrt x + 1}}{{\sqrt x \left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\]
\( = \frac{{\sqrt x - 1 + 2x - \sqrt x - 1}}{{\sqrt x \left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\)\( = \frac{{2x - 2}}{{\sqrt x \left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\)
\( = \frac{{2\left( {x - 1} \right)}}{{\sqrt x \left( {x - 1} \right)}}\)\( = \frac{2}{{\sqrt x }}\).
Vậy với \(x > 0,x \ne 1\) thì \(B = \frac{2}{{\sqrt x }}\).
Lời giải
d) Với \(x > 1,\) ta có:
Xét \(P = \sqrt x + 1 + \frac{2}{{\sqrt x - 1}} = \sqrt x - 1 + \frac{2}{{\sqrt x - 1}} + 2\) với \(x > 1.\)
Do \(x > 1\) nên \(\sqrt x - 1 > 0\).
Áp dụng bất đẳng thức Cauchy, ta có:
\(\sqrt x - 1 + \frac{2}{{\sqrt x - 1}} \ge 2\sqrt {\left( {\sqrt x - 1} \right).\frac{2}{{\sqrt x - 1}}} \)
\(\sqrt x - 1 + \frac{2}{{\sqrt x - 1}} \ge 2\sqrt 2 \)
\(\sqrt x - 1 + \frac{2}{{\sqrt x - 1}} + 2 \ge 2\sqrt 2 + 2\)
Suy ra \(P \ge 2\sqrt 2 + 2\) với \(x > 1\).
Dấu “=” xảy ra khi và chỉ khi \(\sqrt x - 1 = \frac{2}{{\sqrt x - 1}}\) .
Giải phương trình:
\(\sqrt x - 1 = \frac{2}{{\sqrt x - 1}}\)
\({\left( {\sqrt x - 1} \right)^2} = 2\)
\(\sqrt x - 1 = \sqrt 2 \) (do \(\sqrt x - 1 > 0)\)
\(\sqrt x = \sqrt 2 + 1\)
\(x = 3 + 2\sqrt 2 \) (thỏa mãn).
Vậy giá trị nhỏ nhất của \(P = 2\sqrt 2 + 2\) khi \(x = 3 + 2\sqrt 2 \).
Đoạn văn 2
(3,5 điểm)
Lời giải
a) Điều kiện xác định \(x \ne - 1,x \ne 3\).
Ta có: \(\frac{x}{{2\left( {x - 3} \right)}} + \frac{x}{{2x + 2}} = \frac{{2x}}{{\left( {x + 1} \right)\left( {x - 3} \right)}}\)
\(\frac{{x\left( {x + 1} \right)}}{{2\left( {x + 1} \right)\left( {x - 3} \right)}} + \frac{{x\left( {x - 3} \right)}}{{2\left( {x + 1} \right)\left( {x - 3} \right)}} = \frac{{2x \cdot 2}}{{2\left( {x + 1} \right)\left( {x - 3} \right)}}\)
\(x\left( {x + 1} \right) + x\left( {x - 3} \right) = 2x \cdot 2\)
\({x^2} + x + {x^2} - 3x - 4x = 0\)
\(2{x^2} - 6x = 0\)
\(2x\left( {x - 3} \right) = 0\)
\(x = 0\) hoặc \(x - 3 = 0\).
\(x = 0\) (thỏa mãn) hoặc \(x = 3\) (loại).
Vậy phương trình có nghiệm là \(x = 0\).Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
3. Người ta dùng một loại xe tải để chở bia cho một nhà máy. Mỗi thùng bia 24 lon nặng trung bình \(6,7{\rm{ kg}}{\rm{.}}\) Theo khuyến nghị, trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là \(5,25\) tấn.
a) Viết bất phương trình mô tả tình huống trên.
b) Hỏi xe có thể chở được tối đa bao nhiêu thùng bia, biết bác tài xế nặng \(65{\rm{ kg}}{\rm{.}}\)
3. Người ta dùng một loại xe tải để chở bia cho một nhà máy. Mỗi thùng bia 24 lon nặng trung bình \(6,7{\rm{ kg}}{\rm{.}}\) Theo khuyến nghị, trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là \(5,25\) tấn.
a) Viết bất phương trình mô tả tình huống trên.
b) Hỏi xe có thể chở được tối đa bao nhiêu thùng bia, biết bác tài xế nặng \(65{\rm{ kg}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
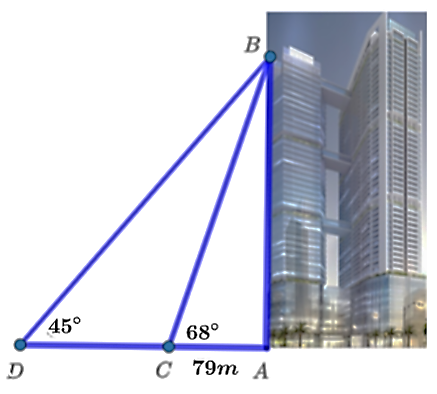
(1,5 điểm) Tháp Discovery Complex A với quy mô 54 tầng, đang là tòa nhà cao nhất quận Cầu Giấy. Tại một thời điểm trong ngày mặt trời tạo với mặt đất một góc xấp xỉ \(68^\circ \) và bóng của tòa nhà trên mặt đất dài khoảng \(79{\rm{ m}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
(2,5 điểm) Cho đường tròn \[\left( O \right)\] và một điểm \[A\] nằm ngoài đường tròn. Từ \[A\] kẻ hai tiếp tuyến \[AB,AC\] (\[B,C\] là các tiếp điểm). Từ \[A\] kẻ đường thẳng cắt đường tròn tại hai điểm \[M\] và \[N\] (điểm \(M\) nằm giữa \(A\) và \(N).\) Gọi \[E\] là trung điểm của dây \[MN\], \[I\] là giao điểm thứ hai của đường thẳng \[CE\] với đường tròn \[\left( O \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập