12 bài tập Góc ở tâm và số đo cung bị chắn có lời giải
30 người thi tuần này 4.6 75 lượt thi 12 câu hỏi 45 phút
🔥 Đề thi HOT:
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
10.8 K lượt thi
5 câu hỏi
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 1: Đại số)
9.9 K lượt thi
188 câu hỏi
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
36 K lượt thi
4 câu hỏi
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
35.9 K lượt thi
3 câu hỏi
Đề kiểm tra giữa học kì 2 môn Toán 9 ( Mới nhất)_ đề 1
19.1 K lượt thi
6 câu hỏi
Tổng hợp đề thi giữa học kì 2 Toán 9 hay nhất năm 2023 có đáp án (Đề 1)
7.5 K lượt thi
5 câu hỏi
Đề thi Giữa học kỳ 2 Toán 9 - Đề 51 có đáp án
13.7 K lượt thi
5 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
A. Góc ở tâm.
B. Góc tạo bởi hai bán kính .
C. Góc bên ngoài đường tròn.
D. Góc bên trong đường tròn.
Lời giải
Đáp án đúng là: A
Góc có đỉnh trùng với tâm đường tròn được góc ở tâm.
Câu 2
A. Có số đo lớn hơn.
B. Có số đo nhỏ hơn 90°.
C. Có số đo lớn hơn 90°.
D. Có số đo nhỏ hơn.
Lời giải
Đáp án đúng là: D
Trong hai cung của một đường tròn hay hai đường tròn bằng nhau, cung nào nhỏ hơn thì có số đo nhỏ hơn.
Câu 3
A. Hai cung bằng nhau nếu chúng đều là cung nhỏ.
B. Hai cung bằng nhau nếu chúng có số đo nhỏ hơn 90°.
C. Hai cung bằng nhau nếu chúng đều là cung lớn.
D. Hai cung bằng nhau nếu chúng có số đo bằng nhau.
Lời giải
Đáp án đúng là: D
Trong hai cung của một đường tròn hay hai đường tròn bằng nhau, hai cung bằng nhau nếu chúng có số đo bằng nhau.
Câu 4
A. 240°.
B. 60°.
C. 180°.
D. 120°.
Lời giải
Đáp án đúng là: D
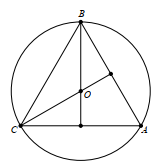
Vì tam giác ABC đều có tâm O là tâm đường tròn ngoại tiếp nên O cũng là giao ba được phân giác nên BO, CO lần lượt là các đường phân giác \(\widehat {ABC},\widehat {ACB}\).
Ta có: \(\widehat {BCO} = \frac{1}{2}\widehat {ACB} = 30^\circ \); \(\widehat {CBO} = \frac{1}{2}\widehat {ABC} = 30^\circ \).
Xét tam giác BOC có \(\widehat {BOC} = 180^\circ - \widehat {CBO} - \widehat {BCO} = 180^\circ - 30^\circ - 30^\circ = 120^\circ \).
Do đó, số đo cung nhỏ BC là 120°.
Cách 2. Ta có: \(\widehat {BOC} = 2\widehat {BAC} = 120^\circ \) (góc nội tiếp và góc ở tâm).
Do đó số đo cung nhỏ BC là 120°.
Câu 5
A. 240°.
B. 60°.
C. 360°.
D. 210°.
Lời giải
Đáp án đúng là: A
Vì tam giác ABC đều có tâm O là tâm đường tròn ngoại tiếp nên O cũng là giao ba được phân giác nên AO, CO lần lượt là các đường phân giác \(\widehat {ABC},\widehat {ACB}\).
Ta có: \(\widehat {CAO} = \frac{1}{2}\widehat {BAC} = 30^\circ \); \(\widehat {ACO} = \frac{1}{2}\widehat {ACB} = 30^\circ \).
Xét tam giác AOC có \(\widehat {AOC} = 180^\circ - \widehat {ACO} - \widehat {CAO} = 120^\circ \)
Do đó, số đo cung nhỏ AC là 120°.
Nên số đo cung lớn AC là: 360° − 120° = 240°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 1
Sử dụng dữ kiện của bài toán dưới đây để trả lời Bài 4, 5
Cho hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M, biết \(\widehat {AMB} = 50^\circ \).
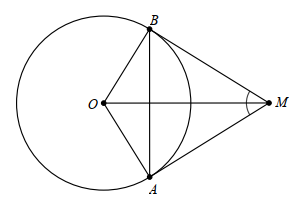
Câu 9
A. \(\widehat {AMO} = 35^\circ ,\widehat {MOB} = 55^\circ \).
B. \(\widehat {AMO} = 65^\circ ,\widehat {MOB} = 25^\circ \).
C. \(\widehat {AMO} = 25^\circ ,\widehat {MOB} = 65^\circ \).
D. \(\widehat {AMO} = 55^\circ ,\widehat {MOB} = 35^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. 130°; 250°.
B. 150°; 250°.
C. 130°; 230°.
D. 150°; 210°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Sử dụng dữ liệu bài toán dưới đây để trả lời Bài 8, 9
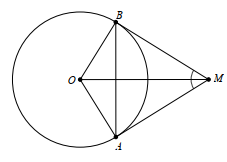
Cho đường tròn (O; R), lấy điểm M nằm ngoài (O) sao cho OM = 2R. Từ M kẻ tiếp tuyến MA và MB với (O) (A, B là các tiếp điểm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo